Java Program to Implement Ackerman Function by Using recursion

Java Program to Find Ackermann Function By Using Recursion

by

Prerequisite: Recursion in Java

In the previous article, we have discussed about Java Program to Calculate Binomial Coefficient by Using Recursion

In this program we are going to see how to find Ackermann function by using Recursion in Java programming language.

Java Program to Find Ackermann Function using Recursion

The Ackermann function is defined for integer x and y:

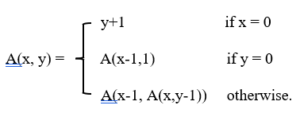
akerman function

Now let’s see different ways to find Ackermann function by using recursion.

Method-1: Java Program to Find Ackermann Function By Using Static Input and Recursion

Approach:

  • Declare and initiate an integer variable ‘x’ as 1
  • Declare and initiate an integer variable ‘y’ as 0
  • Call a user defined method ackermannFunction() and pass the ‘x’ ,‘y’ as parameter.
  • Inside the user defined method we will check the binomial coeffient boundary condition: x==0 then it returns y+1 to the main() method else if y==0 then it calls the ackermannFunction() method recursively.  i.e “ackermannFunction(x-1,1)” and return the value to the main() method else it calls the ackermannFunction() method recursively “ackermannFunction(x-1,ackermannFunction(x,y-1))” and return the value to the main() method.
  • Now the value of the user defined method ackermannFunction() is stored in an integer variable say ‘b’ inside the main() method.
  • Print the value of ackermann function.

Program:

import java.util.*;
import java.io.*;
public class Main 
{
    public static void main(String[] args)
    {
        //declare and initialize an integer variable x
        int x = 1;
        //declare and initialize an integer variable y
        int y = 0;
        //define the method and store the value inside an integer variable say ‘b’
        int b = ackermannFunction(x,y);
        //print the result
        System.out.println("The ackermann function of ("+x+", "+y+") is: "+b);
    }
    
    //ackermannFunction() method
    static int ackermannFunction(int x, int y)
    {
        //checking the ackerman function condition and calling the ackermannFunction() method recursively.
        if(x==0)
            return y+1;
        else if(y==0)
            return ackermannFunction(x-1,1);
        else
            return ackermannFunction(x-1,ackermannFunction(x,y-1));
    }
}

Output:

The ackermann function of (1, 0) is: 2

Method-2: Java Program to Find Ackermann Function By Using User Input and Recursion

Approach:

  • Create a scanner class.
  • Declare two integer variables say ‘x’, ‘y’
  • Prompt the user to enter the values for x, y respectively.
  • Call a user defined method ackermannFunction() and pass the ‘x’ ,‘y’ as parameter.
  • Inside the user defined method we will check the binomial coeffient boundary condition: x==0 then it returns y+1 to the main() method else if y==0 then it calls the ackermannFunction() method recursively.  i.e “ackermannFunction(x-1,1)” and return the value to the main() method else it calls the ackermannFunction() method recursively “ackermannFunction(x-1,ackermannFunction(x,y-1))” and return the value to the main() method.
  • Now the value of the user defined method ackermannFunction() is stored in an integer variable say ‘b’ inside the main() method.
  • Print the value of ackermann function.

Program:

import java.util.*;
import java.io.*;
public class Main 
{
    public static void main(String[] args)
    {
        // create a scanner class
        Scanner s = new Scanner(System.in);
        System.out.println("Enter the value of x:");
        //declare an integer variable ‘x’and initialize it by user input using scanner class.
        int x = s.nextInt();
        System.out.println("Enter the value of y:");
        //declare an integer variable ‘y’and initialize it by user input using scanner class.
        int y = s.nextInt();
        //define the method and store the value inside an integer variable say ‘b’
        int b = ackermannFunction(x,y);
        //print the result
        System.out.println("The ackermann function of ("+x+", "+y+") is: "+b);
    }
    
    //ackermannFunction() method
    static int ackermannFunction(int x, int y)
    {
        //checking the ackerman function condition and calling the ackermannFunction() method recursively.
        if(x==0)
            return y+1;
        else if(y==0)
            return ackermannFunction(x-1,1);
        else
            return ackermannFunction(x-1,ackermannFunction(x,y-1));
    }
}

Output:

Enter the value of x:
2
Enter the value of y:
4
The ackermann function of (2, 4) is: 11

Access the Simple Java program for Interview examples with output from our page and impress your interviewer panel with your coding skills.

Related Java Programs: