Square in c – C Program to Calculate Area and Perimeter of a Square

• Write a C program to find the area and perimeter of a square.

A square is quadrilaterals(having four sides) having all sides equal and all interior angles are 90^.(right angles). Opposite sides of a square are parallel. A square is a special case of parallelogram where all sides and internal angles are equal.
The area of a square is the amount of two-dimensional space inside the boundary on square. The area of a square can be calculated by placing a square shape object over a grid and counting the number of square units it takes to completely fill a square.

The perimeter of a square is the linear distance around the boundary of the square.
In other words, we can think of perimeter of a square surface as the length of fence needed to enclose that square surface, whereas area is the space inside square surface. Perimeter is measured in linear units whereas area is measured in square units.

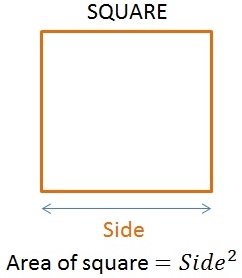
Area of Square To find the area of a square we multiply it’s Side with itself(side square).

• Area of Square = Side X Side

Where Side is the length of any side of square.
Perimeter of Square
To find the perimeter of a square, we should add the length of all four sides of square. As all sides of a square are equal, Hence perimeter of square is equal to 4 times Side of square.

• Perimeter of Square = 4 X S

Where,
S is the length of any side of a square.

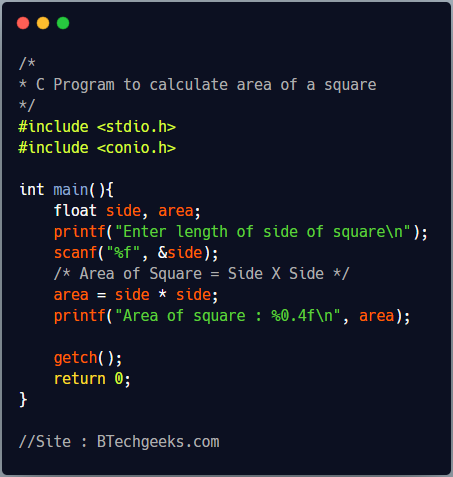
C Program to find the area of a square

Square in c: To calculate area of a square, we need length of any side of a square. Below program, first takes length of side as input from user using scanf function and stores in a floating point variable. To find the area of square we multiple the length of side with itself and store area in a floating point variable. At last, it prints the area of square on screen using printf function.

/*
* C Program to calculate area of a square
*/
#include <stdio.h>
#include <conio.h>
 
int main(){
    float side, area;
    printf("Enter length of side of square\n");
    scanf("%f", &side);
    /* Area of Square = Side X Side */
    area = side * side;
    printf("Area of square : %0.4f\n", area);
     
    getch();
    return 0;
}

Program Output

Enter length of side of square
2.5
Area of square : 6.2500

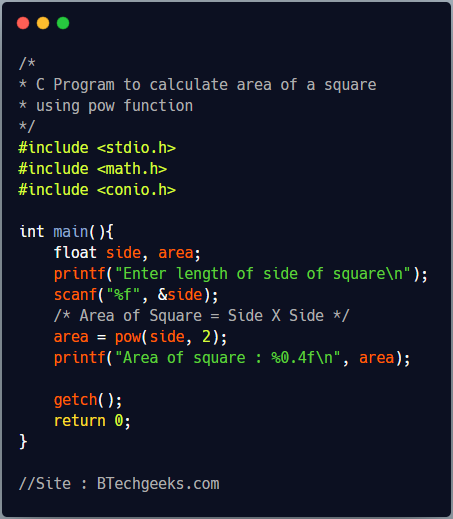
C Program to find the area of a square using pow function

We can use pow function of math.h header file to calculate Side^2(Side square) instead of multiplying Side with itself. double pow(double a, double b) returns a raised to the power of b (a^b). Below program to calculate area of square is same as the above program except that it uses pow function to calculate area.

/*
* C Program to calculate area of a square 
* using pow function
*/
#include <stdio.h>
#include <math.h>
#include <conio.h>
 
int main(){
    float side, area;
    printf("Enter length of side of square\n");
    scanf("%f", &side);
    /* Area of Square = Side X Side */
    area = pow(side, 2);
    printf("Area of square : %0.4f\n", area);
     
    getch();
    return 0;
}

Program Output

Enter length of side of square
4
Area of square : 16.0000

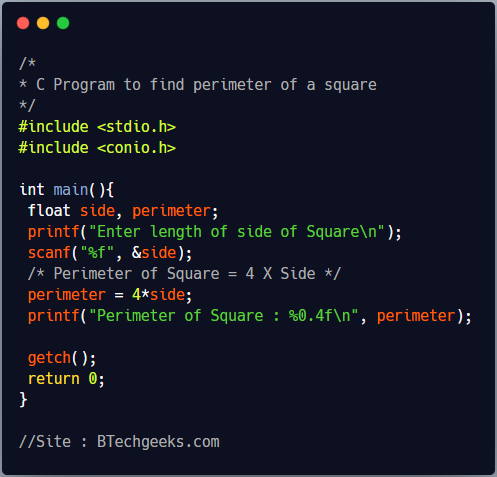
C Program to find the perimeter of a square

To calculate perimeter of a square, we need length of any side of a square. Below program, first takes length of side as input from user using scanf function and stores in a floating point variable named ‘side’. To find the perimeter of square we multiple the length of side with 4(as explained above) and store area in a floating point variable names ‘paremeter’. Then it prints the perimeter of square on screen.

/*
* C Program to find perimeter of a square
*/
#include <stdio.h>
#include <conio.h>
 
int main(){
 float side, perimeter;
 printf("Enter length of side of Square\n");
 scanf("%f", &side);
 /* Perimeter of Square = 4 X Side */
 perimeter = 4*side;
 printf("Perimeter of Square : %0.4f\n", perimeter);
  
 getch();
 return 0;
}

Program Output

Enter length of side of Square
5.0
Perimeter of Square : 20.0000

Properties of Square

• Opposite sides of a square are equal in length and parallel.
• The diagonals of a square bisect each other at right angle.
• The length of diagonals of a square are root 2 times the length of sides.
• The area of square is largest, in compare with any other quadrilateral of same perimeter.