Java Program to Find Length of the chord of the circle whose Radius and the Angle Subtended at the Center by the Chord is Given

In the previous article, we have discussed about Java Program to Find Longest Chord of Circle When Radius is Given

In this article we are going to see how to find length of the chord of the circle whose radius and the angle subtended at the center by the chord is given using Java programming language.

Java Program to Find Length of the chord of the circle whose Radius and the Angle Subtended at the Center by the Chord is Given

Explanation:

Suppose there is a circle with center O and radius r

The angle subtended at the center by its chord PQ = a

i.e. POQ = a (given)

Now, we need to find the length of the chord.

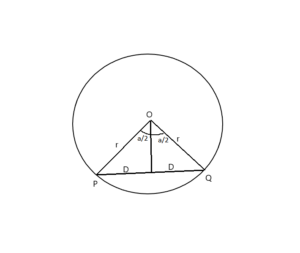
length of the chord PQ = 2D,

Angle subtended by it on the center POQ = a degrees

As the perpendicular bisector from the center bisects the chord

similarly, the perpendicular bisector also bisects the angle equally (a/2)

Using Pythagoras theorem,
D/r = sin((a/2)*π/180 ) ———>(degree converted in radians)

D = r sin((a/2)*π/180)

So, length of the chord PQ = 2D = 2*r* sin((a/2)*3.142/180)

Example:

R = 20
POQ = 90
X = 90/2 = 45
D = r sin((a/2)*3.142/180) = 14.1325
PQ = 2D = 28.27300

Let’s see different ways to find length of the chord of the circle whose radius and the angle subtended at the center by the chord is given.

By Using Static Input Value
By Using User Input Value

Method-1: Java Program to Find Length of the chord of the circle whose Radius and the Angle Subtended at the Center by the Chord is Given By Using Static Value

Approach:

Declare an double variable say ‘r’ and assign the value to it, which holds the radius of the circle.
Declare an double variable say ‘POQ’ and assign the value to it, which holds the angle subtended by the chord at center O.
Find length of D using the formula 2r*sin((a/2)*3.142/180)
Find the length of the chord PQ using the formula 2D
Print the result.

Program:

import java.io.*;
class Main
{
 public static void main(String [] args)
 {
  double r = 20;
  double a =  90;     
  // convert degree to radian
  double D = r*Math.sin((a/2)*(3.14/180));
  double PQ = 2*D;
  System.out.println("The length of the chord PQ is " + PQ);
 }
}

Output

The length of the chord PQ is 28.27300

Method-2: Java Program to Find Length of the chord of the circle whose Radius and the Angle Subtended at the Center by the Chord is Given By Using User Input Value

Approach:

Declare an double variable say ‘r’ which holds the radius of the circle.
Declare an double variable say ‘POQ’ which holds the angle subtended by the chord at center O.
Then we will take the value of “r” and “POQ” as user input using scanner class.
Find length of D using the formula 2r*sin((a/2)*3.142/180)
Find the length of the chord PQ using the formula 2D
Print the result.

Program:

import java.io.*;
import java.util.Scanner;
class Main
{
    public static void main(String [] args)
    {
    // scanner class obj ref
    Scanner s = new Scanner(System.in);  
    // to take user input value
    System.out.println("Enter the radius of the circle ");
    double r = s.nextDouble();                                           
    System.out.println("Enter the subtended angle made by the chord at center O ");
    double a = s.nextDouble();  
    // convert degree to radian
    double D = r*Math.sin((a/2)*(3.14/180));
    double PQ = 2*D;
    System.out.println("The length of the chord PQ is " + PQ);
    }
}

Output:

Enter the radius of the circle 
5
Enter the subtended angle made by the chord at center O 
60
The length of the chord PQ is 4.997701026431025

Related Java Programs: