NP linalg solve - Python NumPy linalg.solve() Function

NumPy linalg.solve() Function:

NP linalg solve: To solve a linear matrix equation or a system of linear scalar equations, use the linalg.solve() function of the NumPy module.

For Example, Consider the system of linear equations shown below:

x + y+ z = 2

6x – 4y + 5z = 31

5x + 2y+ 2z = 13

These equations can be represented in a matrix form as shown below:

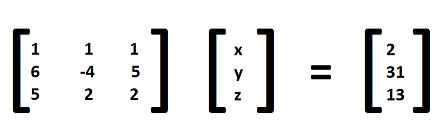
x=3, y=-2, and z=1 are the solutions to the above equations.

As seen in the example below, this can be solved using the numpy.linalg.solve() function.

Syntax:

numpy.linalg.solve(a, b)

Parameters

a: This is required. It is a Coefficient matrix.

b: This is required. It is the ordinate or dependent variable values.

Return Value:

Returns the solution to the ax = b system. The returned shape is the same as b.

NOTE: If “a” is not a square matrix or singular, the LinAlgError exception is thrown.

NumPy linalg.solve() Function in Python

Example

Approach:

Import numpy module using the import keyword.
Pass some random coefficient matrix values as an argument to the array() function to create an array.
Store it in a variable.
Pass some random ordinate/dependent variables values list as an argument to the array() function to create another array.
Store it in another variable.
Pass the above given a, b arrays as the arguments to the linalg.solve function of numpy module to solve the given linear equations.
Store it in another variable.
Print the above result.
The Exit of the Program.

Below is the implementation:

# Import numpy module using the import keyword
import numpy as np
# Pass some random coefficient matrix values as an argument to the
# array() function to create an array. 
# Store it in a variable.
gvn_a_matx = np.array([[1, 1, 1], 
                       [6, -4, 5],
                       [5, 2, 2]])

# Pass some random ordinate/dependent variables values list as an argument to the
# array() function to create another array. 
# Store it in another variable.
gvn_b = np.array([2, 31, 13])
# Pass the above given a, b arrays as the arguments to the linalg.solve function
# of numpy module to solve the given linear equations
# Store it in another variable.
rslt = np.linalg.solve(gvn_a_matx, gvn_b)
# Print the above result
print(rslt)

Output:

[ 3. -2. 1.]

NP linalg solve – Python NumPy linalg.solve() Function

NumPy linalg.solve() Function in Python

Related