We have compiled most frequently asked Python Interview Questions which will help you with different expertise levels.
Python Interview Questions on Trees
There are several types of data structures that can be used to tackle application problems. We have seen how linked lists work in a sequential manner, we have also seen how stacks and queues can be used in programming applications but they are very restricted data structures. The biggest problem while dealing with linear data structure is that if we have to conduct a search, the time taken increases linearly with the size of the data. Whereas there are some cases where linear structures can be really helpful but the fact remains that they may not be a good choice for situations that require high speed.
So, now let’s move on from the concept of linear data structures to nonlinear data structures called trees. Every tree has a distinguished node called the root. Unlike the trees that we know in real life the tree data structure branches downwards from parent to child and every node except the root is connected by a direct edge from exactly one other node.
- Data Structures Lecture Notes PDF | DS Lecture Notes & Study Material PDF Free Download
- Advanced Data Structures and Algorithms Notes and Study Material PDF Free Download
- Search implementations: Linear and Binary
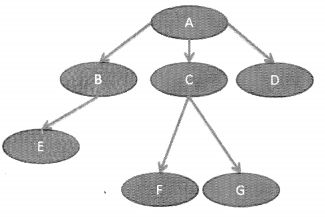
Look at the figure given above:
A is the root and it is parent to three nodes – B, C, and D.
Same way B is a parent to E and C is a parent to F and G.
Nodes like D, E, F, and G that have no children are called leaves or external nodes.
Nodes that have at least child such as B and C are called internal nodes.
The number of edges from the root to the node is called the depth or level of a
node. The depth of B is 1 whereas the depth of G is 2.
The height of a node is the number of edges from the node to the deepest leaf.
B, C, and D are siblings because they have the same parent A. Similarly, F and
G are also siblings because they have the same parent C.
Children of one node are independent of children of another node.
Every leaf node is unique.
- The file system that we use on our computer machines is an example of the tree structure.
- Additional information about the node is known as payload. Payload is not given much importance in algorithms but it plays a very important role in modem day computer applications.
- An edge connects two nodes to show that there is a relationship between them.
- There is only one incoming edge to every node (except the root). However, a node may have several outgoing edges.
- The root of the tree is the only node of the tree that has no incoming edges as it marks the starting point for a tree.
- Set of nodes having incoming edges from the same node are the children of that node.
- A node is a parent of all the nodes that connect to it by the outgoing edges.
- A set of nodes and edges that comprises a parent along with all its descendants are called subtrees.
- A unique path traverses from the root to each node.
- A tree that has a maximum of two children is called a binary tree.
Recursive definition of a tree
A tree can be empty, or it may have a root with zero or more subtree. The root of every subtree is connected to the root of a parent tree by an edge.
Simple Tree Representation
Have a look at the following tree. Here, we are considering the case of a binary tree.
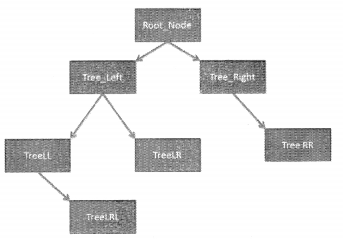
In the case of a binary tree, a node cannot have more than two children. So, for ease of understanding, we can say that the above scenario is similar to something like this:
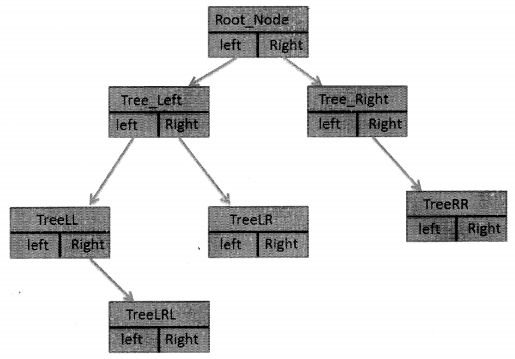
In this diagram, left and right are references to the instances of the node that are located on the left and right of this node respectively. As you can see, every node has three values:
- Data
- Reference to the child on left
- Reference to the child on the right
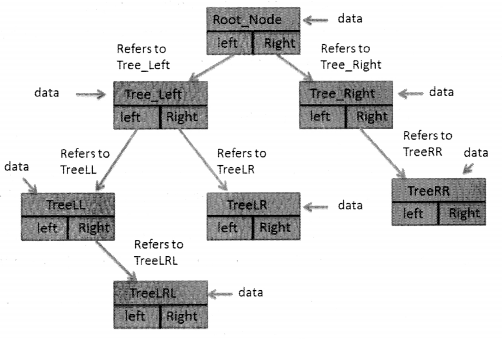
So, the constructor for the node class to create a Node object will be as follows:
class Node(object):
def_init_(self, data_value):
self.data_value = data_value
self.left = None
self.right = None
So, this is how a root node is created:
# Root_Node
print ("Create Root Node")
root = Node("Root_Node")
print("Value of Root = ",root.data_value," left =",root.left, " right = ", root.right)
When we execute this block of code, the output is as follows:
Create Root Node
Value of Root = Root_Node left = None right = None
Value of Node = Tree Left left = None right = None
Now, we write code for inserting values to the left or right. When a node is created, initially it’s left and right reference point to None. So, to add a child to left we just need to say:
self. left = child_node
and a child can be added to right in a similar way:
self.left = child_node
However, if the root node is already pointing to some existing child and we try to insert a child node then the existing child should be pushed down one level and the new object must take its place. So, the reference of the existing child stored in self.left is passed on to child.left and then self.help is assigned the reference to child. This can be achieved in the following manner:
def insert_left (self, child):
if self.left is None :
self.left = child
else:
child.left = self.left
self.left = child
def insert_right(self, child):
if self.right is None:
self.right = child
else :
child.right = self.right
self.right = child
Code
class Node(object):
def_init_(self, data__value) :
self . data_value = data_value
self.left = None
self.right = None
def insert_left(self, child):
if self.left is None:
self.left = child
else:
child.left = self.left
self.left = child
def insert_right(self, child):
if self.right is None:
self.right = child
else:
child.right = self.right
self.right = child
Execution
# Root_Node
print ("Create Root Node")
root = Node("Root_Node")
print("Value of Root = ",root.data_value," left = ",root.left, " right = ", root.right)
#Tree_Left
print("Create Tree_Left")
tree_left = Node("Tree_Left")
root.insert_left(tree_left)
print ("Value of Node = ", tree__left. data_value, " left =",tree_left.left, " right = ",tree_left. right)
print("Value of Root = ", root,data_value," left = ",root.left, " right = ", root.right)
#Tree_Right
print("Create Tree_Right")
tree__right = Node ("Tree_Right")
root.insert_right(tree_right)
print("Value of Node = ",tree_right.data_value, " left =",tree_right.left, " right = ",tree_right. right)
print("Value of Root = " , root. data__value, " left = ",root.left, " right = ", root.right)
#TreeLL
print("Create TreeLL") tree11 = Node("TreeLL")
tree_left.insert_left(tree11)
print("Value of Node = ",tree11.data_value," left =",tree11.left, " right = ",tree11.right)
print("Value of Node = ",tree_left.data_value," left =",tree_left.left, " right = ",tree_left. right)
print("Value of Root = ", root.data_value," left =",root.left, " right = ", root.right)
Output
Create Root Node Value of Root = Root_Node left = None right = None Create Tree_Left Value of Node = Tree_Left left = None right = None Value of Root = Root_Node left = < main .Node object at 0x000000479EC84F60> right = None Create Tree_Right Value of Node = Tree_Right left = None right = None Value of Root = Root_Node left = < main .Node object at 0x000000479EC84F60> right = < main Node object at 0x000000479ED05E80> Create TreeLL Value of Node = TreeLL left = None right = None Value of Node = Tree_Left left = < main .Node object at 0x000000479ED0F160> right = None Value of Root = Root_Node left = < main .Node object at 0x000000479EC84F60> right = < main . Node object at 0x000000479ED05E80>
Question 1.
What is the definition of a tree?
Answer.
A tree is a set of nodes that store elements. The nodes have a parent-child relationship such that:
- If the tree is not empty, it has a special node called the root of the tree. The root has no parents.
- Every node of the tree different from the root has a unique parent node.
Question 2.
Write a code to represent a tree through lists or a list of lists.
Answer:
In the list of lists, we shall store the value of the node as the first element. The second element will be the list that represents the left subtree and the third element represents the right subtree. The following figure shows a tree with just the root node.
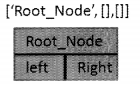
Now, suppose we add a node to the left.
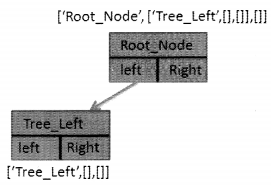
Now, adding another subtree to the right would be equal to:
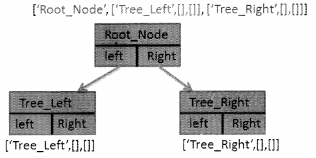
Same way adding a node to the left of Tree Left would mean:
Implement Trees with Lists
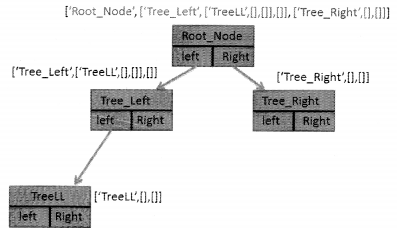
Here you can see that the tree can be defined as follows:
binary_tree = [ ‘Root_Node’ , [ ‘Tree_Left’ ,[ ‘TreeLL’,[ ],[ ] ],[ ] ], [ ‘Tree_Right’,[ ],[ ] ] ]
Here, the root is Root_Node which is located at binary_tree[0].
Left subtree is at binary_tree[1].
The right subtree is at binary_tree[2].
Now let’s write the code for this.
Step 1:
Define Class
class Tree:
Step 2:
Create Constructor
Now let’s write the code for the constructor. Here, when we create an object we pass a value. The constructor creates a list where the value is placed at index 0 and at index 1 and 2 we have two empty lists. If we have to add subtree at the left side we will do so at index 1 and for the right subtree, we will insert values in the list at index 2.
def_init_(self, data): self.tree = [data, [ ],[ ] ]
Step 3:
Define a function to insert left and right subtree
If you have to insert a value in the left subtree then pop the element at index 1 and insert the new list at that place. Similarly, if you have to insert a child on the right-hand side, pop the value at index 2 and insert the new list.
def left_subtree(self,branch):
left_list = self . tree.pop(1)
self.tree.insert(1,branch.tree)
def right_subtree(self,branch):
right_list = self.tree.pop(2)
self.tree.insert(2,branch.tree)
Now, let’s execute the code:
Code
class Tree:
def_init_(self,data):
self.tree = [data, [ ],[ ] ]
def left_subtree(self,branch):
left_list = self.tree.pop(1)
self.tree.insert(1,branch.tree)
def right_subtree(self,branch):
right_list = self.tree.pop(2)
self.tree.insert(2,branch.tree)
Execution
print("Create Root Node")
root = Tree("Root_node")
print("Value of Root = ", root.tree)
print("Create Left Tree")
tree_left = Tree("Tree_Left")
root.left_subtree(tree_left)
print("Value of Tree_Left = ", root.tree)
print("Create Right Tree")
tree_right = Tree("Tree_Right")
root.right_subtree(tree_right)
print("Value of Tree_Right = ", root.tree)
Create Root Node
Value of Root = ['Root_node', [ ], [ ] ]
Create Left Tree
Value of Tree_Left = ['Root_node', ['Tree_Left', [ ] ]/ [ ] ]
Create Right Tree
Value of Tree_Right = ['Root_node', [ 'Tree_Left', [ ], [ ] ], ['Tree_Right', [ ], [ ] ] ]
Create Terrell
Value of Tree_Left = ['Root_node', ['Tree_Left', [ 'TreeLL', [ ], [ ] ], [ ] ], ['Tree_Right', [ ], [ ] ] ]
>>>
There is however one thing ignored in this code. What if we want to insert a child somewhere in between? Here, in this case the child will be inserted at the given location and the subtree existing at that place will be pushed down.
For this we make changes in the insert functions.
def left_subtree(self,branch):
left_list = self.tree.pop(1)
if len(left_list) > 1:
branch.tree[1]=left_list
self.tree.insert (1,branch.tree)
else:
self.tree.insert(1,branch.tree)
If we have to insert a child in the left then first we pop the element at index 1. If the length of element at index 1 is 0 then, we simply insert the list. However, if the length is not zero then we push the element to the left of the new child. The same happens in case of right subtree.
def right_subtree(self,branch):
right_list = self.tree.pop (2)
if len(right_list) > 1:
branch.tree[2]=right_list
self.tree.insert(2,branch.tree)
else:
self.tree.insert(2,branch.tree)
print ("Create TreeLL")
tree11 = Tree("TreeLL")
tree_left.left_subtree(tree11)
print("Value of Tree_Left = ", root.tree)
Code
class Tree:
def_init_(self,data) :
self.tree = [data, [ ], [ ] ]
def left_subtree(self,branch):
left_list = self.tree.pop(1)
if len(left_list) > 1:
branch.tree[1]=left_list
self.tree.insert (1,branch.tree)
else:
self.tree.insert(1,branch.tree)
def right_subtree(self,branch):
right_list = self.tree.pop(2)
if len(right_list) > 1:
branch.tree[2]=right_list
self.tree.insert(2,branch.tree)
else:
self.tree.insert(2,branch.tree)
Execution
print ("Create Root Node")
root = Tree("Root_node")
print("Value of Root = ", root.tree)
print("Create Left Tree")
tree_left = Tree("Tree_Left")
root.left_subtree(tree_left)
print("Value of Tree_Left = ", root.tree)
print("Create Right Tree")
tree_right = Tree("Tree_Right")
root.right_subtree(tree_right)
print("Value of Tree_Right = ", root.tree)
print("Create Left Inbetween")
tree_inbtw = Tree("Tree left in between")
root.left_subtree(tree_inbtw)
print("Value of Tree_Left = ", root.tree)
print("Create TreeLL")
treell = Tree("TreeLL")
tree_left.left_subtree(tree11)
print("Value of TREE = ", root.tree)
Output
Create Root Node Value of Root = ['Root node', [ ], [ ] ] Create Left Tree Value of Tree Left = [ 'Root node', [ 'Tree Left', [ ], [ ] ], [ ] ] Create Right Tree Value of Tree Right = [ 'Root node' , [ 'Tree Left', [ ] , [lie 1 'Tree Right', [], [ ] ] ] Create Left Inbetween Value of Tree Left = [ 'Root node' , [ 'Tree left in between' , [ 'Tree Left', [ ] , [ ] ] , [ ] ] , ['Tree_Right', [ ], [ ] ] ] Create TreeLL Value of TREE = [ 'Root node', [ 'Tree left in between' , ['Tree Left' , [ 'TreeLL', [ ], [ ] ], [ ]], ['Tree_Right', [ ], [ ] ] ] >>>
Question 3.
What is a binary tree? What are the properties of a binary tree?
Answer:
A data structure is said to be a binary tree if each of its nodes can have at most two children. The children of the binary tree are referred to as the left child and the right child.
Question 4.
What are tree traversal methods?
Answer:
Traversals
Preorder Traversal: First visit the root node, then visit all nodes on the left followed by all nodes on the right.
Code
class Node(object) :
def_init_(self, data_value):
self.data_value = data_value
self.left = None
self.right = None
def insert_left(self, child):
if self.left is None:
self.left = child
else:
child.left = self.left
self.left = child
def insert_right(self, child):
if self.right is None:
self.right = child
else:
child.right = self.right
self.right = child
def preorder(self, node):
res= [ ]
if node:
res.append(node.data_value)
res = res + self.preorder(node.left)
res = res + self.preorder(node.right)
return res
Execution
# Root_Node
print("Create Root Node")
root = Node("Root_Node")
#Tree_Left
print ("Create Tree_Left")
tree_left = Node("Tree_Left")
root.insert_left(tree_left)
#Tree_Right
print("Create Tree_Right")
tree_right = Node("Tree_Right")
root.insert_right(tree_right)
#TreeLL
print ("Create TreeLL")
treell = Node("TreeLL")
tree_left.insert_left(treell)
print("*****Preorder Traversal*****")
print(root.preorder(root))
Output
Create Root Node Create Tree_Left Create Tree_Right Create TreeLL *****Preorder Traversal***** ['Root_Node', 'Tree_Left', 'TreeLL', 'Tree_ Right'] >>>
In Order Traversal :First visit all nodes on the left then the root node and then all nodes on the right..
class Node(object):
def_init_(self, data_value):
self.data_value = data_value
self.left = None
self.right = None
def insert_left(self, child):
if self.left is None:
self.left = child
else:
child.left = self.left
self.left = child
def insert_right(self, child):
if self.right is None:
self.right = child
else:
child.right = self.right
self.right = child
def inorder(self, node):
res=[ ]
if node:
res = self.inorder(node.left)
res.append(node.data_value)
res = res + self.inorder(node.right)
return res
# Root_Node
print("Create Root Node")
root = Node("Root_Node")
#Tree_Left
print ("Create Tree_Left")
tree_left = Node("Tree_Left")
root.insert_left(tree_left)
#Tree_Right
print("Create Tree_Right")
tree_right = Node("Tree_Right")
root.insert_right(tree_right)
#TreeLL
print("Create TreeLL")
treell = Node ("TreeLL")
tree_left.insert_left (treell)
print("*****Inorder Traversal*****)
print(root.inorder(root))
Output
Create Root Node Create Tree_Left Create Tree_Right Create TreeLL *****Inorder Traversal***** *****Inorder Traversal***** *****Inorder Traversal***** *****Inorder Traversal***** *****Inorder Traversal***** *****Inorder Traversal***** *****Inorder Traversal***** *****Inorder Traversal***** *****Inorder Traversal***** ["TreeLL' , 'Tree_Left' , 'Root_Node' , 'Tree_Right'] >>>
Post order Traversal: Visit all nodes on the left, then visit all nodes on the right , then visit the root node.
code
class Node(object):
def_init_(self, data_value):
self.data_value = data_value
self.left = None
self.right = None
def insert_left (self, child):
if self.left is None:
self.left = child
else:
child.right = self.right
self.right = child
def postorder (self, node):
res = [ ]
if node:
res = self.postorder (node.left)
res = res + self.postorder (node.right)
res.append (node.data_value)
return res
Execution
#Root_Node
print("Create Root Node")
root = Node ("Root_Node")
#Tree_Left
print("Create Tree_Left")
tree_left = Node("Tree_Left")
root.insert_left(tree_left)
#Tree_Right
print("Create Tree_Right")
tree_right = Node("Tree_Right")
root . insert_right(tree_right)
#TreeLL
print ("Create TreeLL")
tree11 = Node ("TreeLL")
tree_left . insert_left(tree11)
print("*****postorder Traversal *****")
print (root.postorder (root))
OUTPUT
Create Root Node
Create Tree_Left
Create Tree_Right
Create TreeLL
*****Postorder Traversal*****
['TreeLL' , 'Tree_Left' , 'Tree_Right' , "Root_Node']
A binary heap is a binary tree. It is a complete tree, which means that all levels are completely filled except possibly the last level. It also means that the tree is balanced
As every new item is inserted next to the available space. A Binary heap can be stored in an array.
A binary heap can be of two types: Min Heap or Max Heap. In case of Min Heap binary heap, the root node is the minimum of all the nodes in the binary heap,all parent nodes are smaller than their children. On the other hand in case of Max Heap the root is the maximum among all the keys present in the heap and and all nodes are bigger than their children.
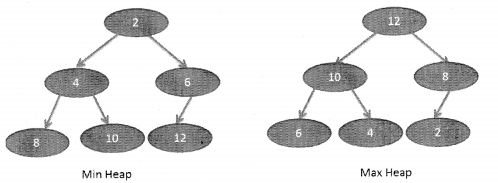
Heap has two important properties:
1. It is complete and is constructed from left to right across each row and the last row may not be completely full. Each row should be filled
up sequentially. So, the order of inserting values should be from left to right, row by row sequentially as shown in the following figure:
2. The parent must be larger (Max Heap)/smaller(Min Heap) than the children.
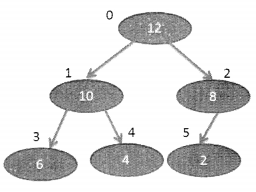
Look at the figure shown above, it is a case of Maximum heap because all parents are greater than their children.
The binary heap can be represented in an array as follows:
0 1 2 3 4 5

If you look at the array carefully you will realize that if a parent exists at location n then the left child is at 2n+l and the right child is at 2n + 2. ”
n= 0
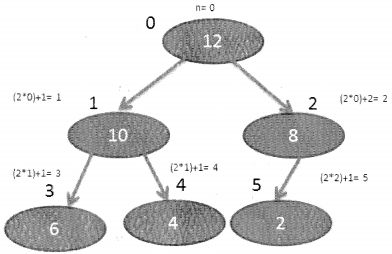
So, if we know the location of the parent child we can easily find out the location of the left and right child.
Now suppose we have to build up a Max Heap using following values: 20,4, 90, 1, 125
Step 1:
Insert 20

Step 2:
Insert 4 -> Left to Right-> First element in second row
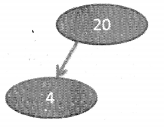
Since the parent is greater than the child, this is fine.
Step 3:
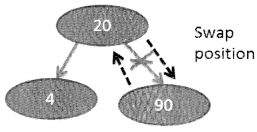
Insert 90 -> Left to Right -> Second element in second row
However when we insert 90 as the right child, it violates the rule of the max heap because the parent has a key value of 20. So, in order to resolve this problem it is better to swap places as shown in the following figure:
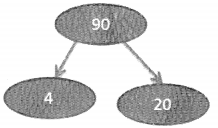
After swapping, the heap would look something like this:
Step 4:
Insert 1 -> left to right -> first element third row
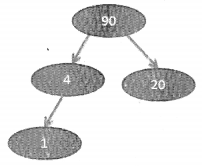
Since 1 is smaller than the parent node, this is fine.
Step 5:
Insert 125
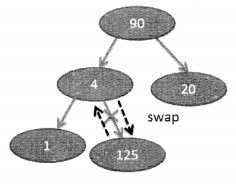
This violated the rule of Max Heap Swap 4 and 125
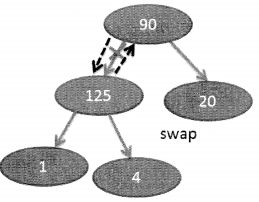
Not a heap still Swap 125 and 90
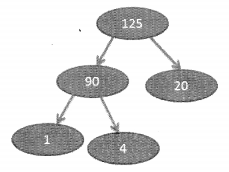
We now have a Max Heap.
Question 5.
Write python code to implement Max Heap. How would you insert a value so that the root node has the maximum value and all parents are greater than their children.
Answer:
Here we will write The code to implement Maxheap class. The class will have two functions:
Push( ) : To insert value.
FIoat_up( ): To place the value where it belongs.
Step 1
Define the class
class MaxHeap:
Step 2
Define The Constructor
def init (self): self.heap = [ ]
Step 3
Define the push( ) function
The push function does two jobs:
- Appends the value at the end of the list. (We have seen earlier that the value has to be inserted first at the available location)
- After appending the value, the push() function will call the float_ up(index) function. The pushQ function passes the index of the last element to the float_up() function so that the float_up() function can analyse the values and do the needful as described in the next step.
def push(self,value):
self.heap.append(value)
self .floatj_up (len (self . heap) -1)
Step 4
Define the float_up function
1. The float_up( )function takes index value as parameter.
def float_up (self, index) :
2. The push( ) function passes the index value of the last element in the heap. The first thing that the float function does is that it checks if the element is at index 0 or not. If yes, then it is the root node. Root node has no parents and since it’s the last element of the heap it has no children either. So, we can return the value.
if index==0: return
3. If the index is greater than 0 then we can proceed further. Look the following figure once again:
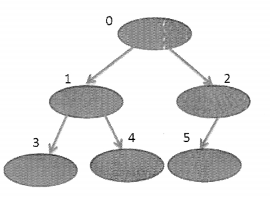
For programming, you need to understand few things:
The index 0 has two children at position 1 and 2. If I have an element at 1 then I can find the parent by calculating value of (1//2). Similarly for element at index 2, the parent’s index value can be found out by calculating value of (2//2 -1). So, we can say that if an element has an index value index and it is odd then it’s parent’s index value, parent_ ofindex = index//2. However, if index is even parentofindex will be (index//2)-1. This becomes the outer frame for the float_up function. The right child has an even number as index and the left child has an odd number as index.
if index==0:
return
else:
if index%2==0:
parent_of_index = (index//2)-l
----------write code----------
else:
parent_of_index = index//2
----------write code--------
4. Now, we compare the values of the child and the parent. If the child is greater than the parent, swap the elements.
def float_up (self, index) :
if index==0:
return
else:
if index%2==0:
parent_of_index = (index//2)-1
if self.heap[index]> self, heap[parent_of_index]:
self.swap(index, parent_of_index)
else:
parent_of_index = index//2
if self.heap[index]> self, heap[parent_of_index]:
self.swap(index, parent_of_index)
self.float_up (parent_of_index)
Step 5
Define the swap function
The swap( ) function helps in swapping the values of the parent and the child, the code for this is given as follows:
def swap(self,indexl, index2):
temp = self.heap[index1]
self.heap[index1] = self.heap[index2]
self.heap[index2] = temp
Code
class MaxHeap:
def_init_(self):
self.heap = [ ]
def push(self,value):
self.heap.append(value)
self .float_up (len (self .heap) -1)
def float_up (self, index) :
if index==0:
return
else:
if index%2==0:
parent_of_index = (index//2)-1
if self.heap[index]> self, heap[parent_of_index]:
self.swap(index, parent_of_ index)
else:
parent_of_index = index//2
if self.heap[index]> self, heap[parent_of_index]:
self.swap(index, parent_of_index)
self .float_up (parent_of_index)
def peek(self):
print(self.heap[0])
def pop(self):
if len(self.heap)>=2:
temp = self.heap[0]
self.heap[0]=self.heap[len(self.heap)-1]
self.heap[len(self.heap)-1]
self.heap.pop( )
self.down_adj( )
elif len(self.heap)==1:
self.heap.pop( )
else:
print("Nothing to pop")
def swap(self,indexl, index2):
temp = self.heap[index1]
self.heap[indexl] = self.heap[index2]
self.heap[index2] = temp
Execution
H = MaxHeap( )
print("*****pushing values***********")
print("pushing 165")
H.push(165)
print(H.heap)
print("pushing 60")
H.push (60)
print(H.heap)
print("pushing 179")
H.push(179)
print(H.heap)
print("pushing 400")
H.push(400)
print(H.heap)
print("pushing 6")
H.push(6)
print(H.heap)
print("pushing 275")
H.push(275)
print(H.heap)
Output
*****pushing values*********** pushing 165 [165] pushing 60 [165, 60] pushing 179 [179, 60, 165] pushing 400 [400, 179, 165, 60] pushing 6 [400, 179, 165, 60, 6] pushing 275 [400, 179, 275, 60, 6, 165] >>>
Question 6.
Write code to find out the maximum value in the Max heap.
Answer:
It is easy to find the max value in the max heap as the maximum value is available at the root node which is index 0 of the heap.
def peek(self): print(self.heap[0])
Question 7.
Write the code to pop the maximum value from Max Heap.
Answer:
There are two steps involved:
- Swap the root with the last element in the array and pop the value.
- The root node now does have the maximum value. So, now we need to move downwards, comparing the parent with their left and right child to ensure that the children are smaller than the parent. If not we will have to swap places again.
Step 1
Define pop( ) function.
The pop( ) function which swaps the values of the root node with the last element in the list and pops the value. The function then calls the down_ adj( ) function which moves downwards and adjusts the values. The pop() function first checks the size of the heap. If the length of the heap is 1 then that means that it only contains one element that’s the root and there is no need to swap further.
def pop(self):
if len(self.heap)>2:
temp = self.heap[0]
self.heap[0]=self.heap[len(self.heap)—1]
self.heap[len(self.heap)-1]
self.heap.pop ( )
print("heap after popping largest value =", self.heap)
self.down_adj( )
elif len(self.heap)==1:
self.heap.pop( )
else:
print("Nothing to pop")
Step 2:
Define downadj( ) function
Set Index Value To 0.
Index of left child = left_child = index*2+1 Index of right child = right child = index*2+2
Then we go through loop where we check the value of the parent with both left and right child. If the parent is smaller than the left child then we swap the value. We then compare the parent value with the right child, if it is less then we swap again.
This can be done as follows:
- Check if parent is less than left child:
- If yes, check if left child is less than the right child
- if yes, then swap the parent with the right child
- Change the value of index to value of right_child for further assessment
- If no the just swap the parent with the left child
- Set the value of index to value of left_child for further assessment
- If the parent is not less than left child but only less than the right child then swap values with the right child
- Change the value of index to right_child
def down_adj(self):
index = 0
for i in range(len(self.heap)//2):
left_child = index*2+1 .
if left_child > len (self.heap) :
return
print("left child = ", left_child)
right_child = index*2+2
if right_child > len (self.heap) :
return
print("right child = ", right_child)
if self.heap[index]<self.heap[left_child]:
temp = self.heap[index]
self.heap[index] = self.heap[left_child]
self.heap[left_child] = temp
index = left_child
if self.heap[index]<self.heap[right_child]:
temp = self.heap[index]
self.heap[index] = self.heap[right_child]
self.heap[right_child] = temp
index = right_child
Code
class MaxHeap:
def_init_(self):
self.heap = [ ]
def push(self,value):
self.heap.append(value)
self .float_up (len (self, heap) -1)
def float_up (self, index) :
if index==0:
return
else:
if index%2==0:
parent_of_index = (index//2)-1
if self.heap[index]> self, heap[parent_of_index]:
temp = self.heap[parent_of_index]
self.heap[parent_of_index] =self.heap[index]
self.heap[index] = temp
else:
parent_of_index = index//2
if self.heap[index]> self, heap[parent_of_index]:
temp = self.heap[parent_of_index]
self.heap[parent_of_index] = self.heap[index]
self.heap[index] = temp self.float_up (parent_of_index)
def peek(self):
print(self.heap [0])
def pop(self):
if len(self.heap)>=2:
temp = self.heap[0]
self.heap[0]=self.heap[len(self.heap)-1]
self.heap[len(self.heap)-1]
self.heap.pop( )
self.down_adj( )
elif len(self.heap)==1:
self.heap.pop ( )
else:
print ("Nothing to pop")
def swap(self,indexl, index2):
temp = self.heap[index1]
self.heap[indexl] = self.heap[index2]
self.heap[index2] = temp
def down_adj(self):
index = 0
for i in range(len(self.heap)//2):
left_child = index*2+1
if left_child > len(self.heap)-1:
print(self.heap)
print("End Point")
print("Heap value after pop( ) =",self.heap)
return
right_child = index*2+2
if right_child > len(self.heap)-1:
print ("right child does not exist")
if self.heap[index]<self.heap[left_child]:
self.swap(index,left_child)
index = left_child
print("Heap value after pop( ) =", self.heap)
return
if self.heap[index]<self.heap[left_child]:
if self.heap[left_child]<self. heap[right_child]:
self.swap(index,right_child) index = right_child
else:
self.swap(index,left_child) index = left_child
elif self.heap[index]<self.heap[right_child]:
self.swap(index,right_child) index = right_child
else:
print("No change required" )
print("Heap value after pop() = ", self.heap)
Execution
H = MaxHeap( )
print("*****pushing values***********")
H.push (165)
print(H.heap)
H.push(60)
print(H.heap)
H.push(179)
print(H.heap)
H.push(400)
print(H.heap)
H.push(6)
print(H.heap)
H.push(275)
print(H.heap)
print("*********popping values*******")
H.pop ( )
H.pop( )
H.pop ( )
H.pop ( )
H.pop ( )
H.pop ( )
H.pop ( )
Output
pushing values [165] [165, 60] [179, 60, 165] [400, 179, 165, 60] [400, 179, 165, 60, 6] [400, 179, 275, 60, 6, 165] *********popping values******* [275, 179, 165, 60, 6] End Point Heap value after pop( ) = [275, 179, 165, 60, 6] right child does not'exist Heap value after pop() = [179, 60, 165, 6] Heap value after pop() = [165, 60, 6] right child does not exist Heap value after pop() = [60, 6] Heap value after pop () = [6] Nothing to pop >>>
Question 8.
Time complexity for max heap:
Answer:
- Insert: 0(log n)
- Get Max: 0(1) because the maximum value is always the root at ‘ index( )
- Remove Max: 0(log n)
The implementation of Min Heap is similar to Max Heap just that in this case the root has the lowest value and the value of parent is less than the left and right child.
Code
class MinHeap:
def_init_(self):
self.heap = [ ]
def push(self,value):
self.heap.append(value)
self .float_up (len (self .heap) -1)
def float_up (self, index) :
if index==0:
return
else:
if index%2==0:
parent_of_index = (index//2)-1
if self.heap[index]< self, heap[parent_of_index]:
self.swap(index, parent_of_index)
else:
parent_of_index = index//2
if self.heap[index]< self, heap[parent_of_index]:
self.swap(index, parent_of_index)
self .floatyup (parent_of_index)
def peek(self) :
print(self.heap [0])
def pop (self) :
if len(self.heap)>=2:
temp = self.heap[0]
self.heap[0]=seIf.heap[len(self.heap)-1]
self.heap[len(self.heap)-1]
self.heap.pop ( )
self.down_adj( )
elif len(self.heap)==1:
self.heap.pop()
else:
print("Nothing to pop")
def swap(self,indexl, index2):
temp = self.heap[index1]
self.heap[indexl] = self.heap[index2]
self.heap[index2] = temp
Execution
H = MinHeap( )
print("*****pushing values***********")
print("pushing 165")
H.push (165)
print(H.heap)
print("pushing 60")
H.push(60)
print(H.heap)
print("pushing 179")
H.push(179)
print(H.heap)
print("pushing 400")
H.push(400)
print(H.heap)
print("pushing 6")
H.push (6)
print(H.heap)
print("pushing 275")
H.push(275) '
print(H.heap)
Output
*****pushing values*********** pushing 165 [165] pushing 60 [60, 165] pushing 179 [60, 165, 179] pushing 400 [60, 165, 179, 400] pushing 6 [6, 60, 179, 400, 165] pushing 275 [6, 60, 179, 400, 165, 275] >>>
Question 9.
What are the applications of binary heap?
Answer:
- Dijkstra Algorithm
- Prims Algorithm
- Priority Queue
- Can be used to solve problems such as:
- K’th Largest Element in an array
- Sort an almost sorted array
- Merge K Sorted Array
Question 10.
What is a priority queue and how can it be implemented?
Answer:
Priority queue is like a queue but it is more advanced. It has methods same as a queue. However, the main difference is that it keeps the value of higher priority at front and the value of lowest priority at the back. Items are added from the rear and removed from the front. In priority queue elements are added in order. So, basically there is a priority associated with every element. Element of highest priority is removed first. Elements of equal priority are treated ass per their order in queue.
Binary heap is the most preferred way of implementing priority queue as they can retrieve the element of highest priority in 0(1) time. Insert and delete can take O(logn) time. Besides that since, the binary heap use lists or arrays, it is easy to locate elements and the processes involved are definitely quite cache friendly. Binary heaps do not demand extra space for pointers and are much easier to insert.
