We have compiled most frequently asked Python Interview Questions which will help you with different expertise levels.
Python Interview Questions on Recursion
When a function makes a call to itself it is called recursion. The same sets of instructions are repeated again and again for new values and it is important to decide when the recursive call must end. For Example: Let’s look at the code to find the factorial of a number.
If we use a loop then a factorial function would look something like this:
Code
def factorial(number):
j = 1
if number==0|number==1:
print(j)
else:
for i in range (1, number+1):
print(j," * ",i," = ",j*i)
j = j*i
print(j)
Execution
factorial(5)
Output
1 * 1 = 1 1 * 2 = 2 2 * 3 = 6 6 * 4 = 24 24 * 5 = 120 120 >>>
- Python Program to Count Divisors of Factorial
- Python Program to Print Numbers in a Range (1,upper) Without Using any Loops or by Using Recursion
- Python Program to Find if a Number is Prime or Not Prime Using Recursion
Now, let’s have a look at how we can solve the same problem using a recursive algorithm.
Code
def factorial(number):
j = 1
if number==0 | number==1:
return j
else:
return number*factorial(number-1)
Execution
print(factorial(4))
Output
24
Pros and Cons
Recursive functions make the code look neat, it helps in breaking a complex task into simpler sub-problems. It can be easier than implementing iterations. However, it can be a little difficult to understand the logic behind recursion. Recursion can consume more memory and time and can be hard to debug.
Question 1.
Write code to find the sum of natural numbers from 0 to the given number using recursion.
Answer:
| I | Result |
| 0 | 0 |
| 1 | 1+0=i(1)+i(0)=1 |
| 2 | 2+1=i+i(1)=3 |
| 3 | 3+3=i+i(2)=6 |
| 4 | 4+6=i+i(3)=10 |
| 5 | 5+10=i+i(4)=15 |
Observe for i = 0, the result is 0, thereafter result = i(n)+i(n-l)
Code
def natural sum(num):
if num == 0
return 0
else:
return (num + natural sum(num-1) )
Execution
print (natural_sum(10))
Output
55
Question 2.
What would be the output for the following code?
def funny (x,y):
if y == 1:
return x [0]
else:
a = funny (x, y-1)
if a>x [y-1]
return a
else:
return x[y-1]
x = [1,5,3,6,7]
y = 3
print (funny (x,y) )
Answer:
If we insert a print statement in the code and execute the code again we can see the actual sequence in which it executes:
def funny(x,y):
print("calling funny , y = ",y)
if y == 1:
return x[0]
else:
print("inside else loop because y = ", y)
a = funny(x, y-1)
print("a = ", a)
if a > x[y-1]:
print("a = ",a, " Therefore a > ",x[y-1])
return a
else:
print("a = ",a, " Therefore a < ",x[y-1])
return x[y-1]
x = [1,5,3,6,7]
y = 3
print(funny(x,y))
Output
calling funny , y = 3 inside else loop because y = 3 calling funny , y = 2 inside else loop because y = 2 calling funny , y = 1 a = 1 a = 1 Therefore a < 5 a = 5 a = 5 Therefore a > 3 5 The answer is 5
Question 3.
What would be the output of the following code?
def funny(x): if (x%2 == 1) : return x+1 else: return funny(x-1) print(funny(7)) print(funny(6))
Answer:
For x =7
1. x = 7
2. x % 2 is 1
return 7 + 1
For x = 6
1. x =6
2. x%2 = 0
3. Return funny(5)
4. x = 5 .
5. x%2 =1
6. Return x+1 = 6
Question 4.
Write Fibonacci sequence using recursion. Answer:
The Fibonacci sequence = 0, 1, 2, 3, 5, 8, 13 ……….
| I | Result |
| 0 | 0 |
| 1 | 1 |
| 2 | 1+0=i(0)+i(1)=1 |
| 3 | 1+1=i(2)+i(1)=2 |
| 4 | 2+1=i(3)+i(2)=3 |
| 5 | 3+2=i(4)+i(3)=5 |
Observe for i = 0, the result is 0 and for i = 1, the result is 1. Thereafter, the value of i(n) = i(n-1) + i(n-2). We implement the same, when we try to find Fibonacci code using recursion.
- The fibonacci_seq(num), takes a number as argument.
- If num = 0, result is 0
- If num = 1, result is 1
- Else result is fibonacci_seq(num-l) + Fibonacci_seq(num-2)
- If you want to find Fibonacci Sequence for 10 then:
- For elements 0 to 10 o Call the fibonacci_seq( ) function
- fibonacci_seq(0) = 0
- fibonacciseq(l) = 1
- fibonacci_seq(2) = fibonacci_seq(l)+ fibonacci_seq(0)
- fibonacci_seq(3) = fibonacci_seq(2)+ fibonacci_seq(3)
Code
def fibonacci_seq (num) :
if num <0:
print("Please provide a positive integer value")
if num == 0:
return 0
elif num == 1:
return 1
else:
return (fibonacci_seq (num-1) +fibonacci_ seq(num-2))
Execution
for i in range(10):
print (fibonacci_seq(i))
Output
0 1 1 2 3 5 8 13 21 34
Question 5.
What is memoization?
Answer:
Basically, in memoization, we maintain a look-up table where solutions are stored so that we don’t have to solve the same sub-problem again and again. Instead, we solve it once and store the values so that they can be reused.
We know that Fibonacci sequence is:
F(n) = F(n-1)+F(n-2) if n>1 = n if n =0,1
So,
F(n):
if n<1:
return n
else :
return F(n-1)+F(n-2)
Here, we are making two recursive calls and adding them up and the value is returned.
Look at the following diagram:
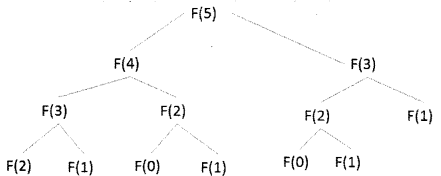
Just to find Fibonacci(5), Fibonacci(2) is computed three times and Fibonacci (3) is computed two times. So, as n increases Fibonacci function’s performance will go down. The consumption of time and space would increase exponentially with an increase in n. In order to save time what we can do is save a value when it is computed for the first time. So, we can save F(2) when it is computed for the first time, the same way with F(3), F(4)… so on. So, we can say that:
F(n): if n=<1: return n elif f(n) exist: return F(n-1) else: F(n) = F(n-1) + F(n-2) save F(n). Return F(n).
In the code below:
- The function Fibonacci( ) takes a number and creates a list, fib_num of size num+1. This is because the Fibonacci series starts from 0.
- It calls the function fib_calculate( )which takes the number num and lists fib_num as a parameter.
- We have saved-I at all index in the list:
a. If fib_num[num] is>0, that means Fibonacci for this number already exists and we need not compute it again and the number can be returned.
b. If num <= 1 then return num.
c. Else if num >=2, calculate fib_calculate(num – 1, fib num) + fib_calculate(num – 2, fib_num). The value calculated must be stored in list fib_num at index num so that there is no need to calculate it again.
Code
def fibonacci (num) :
fib_num = [-1] * (num + 1)
return fib_calculate (num, fib_num)
def fib_calculate (num, fib_num) :
if fib_num [num] >= 0:
return fib_num[num]
if (num <= 1):
fnum = num
else:
fnum = fib_calculate (num - 1, fib_num) + fib_ calculate (num - 2, fib_num)
fib_num [num] = fnum
return fnum
Execution
num = int(input('Enter the number: '))
print ("Answer = ", fibonacci (num) )
Output
Enter the number: 15 Answer = 610 >>>
Question 6.
What would be the output of the following program?
def test_function(i, j) :
if i == 0:
return j;
else:
return test_function(i-1, j+1)
print (test_function(6,7) )
Answer:
| I | J | I==0? | Return |
| 6 | 7 | No | Test_function(5,8) |
| 5 | 8 | No | Test_function(4,9) |
| 4 | 9 | No | Test_function(3,10) |
| 3 | 10 | No | Test_function(2,11) |
| 2 | 11 | No | Test_function(1,12) |
| 1 | 12 | No | Test_function(0,13) |
| 0 | 13 | Yes | 13 |
The output will be 13.
Question 7.
What will be the output for the following code:
def even(k):
if k <= 0:
print("please enter a positive value")
elif k == 1:
return 0
else:
return even(k-1) + 2
print(even(6))
Answer:
| K | K<=0 | K ==1 | Result |
| 6 | no | No | Even(5)+2 |
| 5 | No | No | Even(4)+2+2 |
| 4 | No | No | Even(3)+2+2+2 |
| 3 | No | No | Even(2)+2+2+2+2 |
| 2 | No | No | Even(1)+2+2+2+2+2 |
| 1 | No | yes | 0)+2+2+2+2+2 |
Question 8.
Write a code to find the n_power(n), of 3 using recursion. Answer:
1. Define function n_power(n), it takes the value of power and parameter(n).
2. If n = 0 then return 1 because any number raised to power 0 is 1.
3. Else return (n_power(n-1)).
| N | N<0 | N ==0 | Result |
| 4 | No | No | n_power(3)*3 |
| 3 | No | No | n_power(2)*3*3 |
| 2 | No | No | n_power(1)*3*3*3 |
| 1 | No | No | n_power(0)*3*3*3*3 |
| 0 | No | Yes | 1*3*3*3*3 |
Code
def n_power(n):
if n < 0:
print ("please enter a positive value")
elif n == 0:
return 1
else:
return n_power(n-1)*3
Execution
print(n_power(4))
Output
81
