Computer Science Probability MCQ Quiz Questions and Answers PDF Download
![]()
Question 1.
Let A and B be any two arbitrary events, then, which one of the following is true?
(a) P (A ∩ B) = P(A) P(B)
(b) P (A ∪ B) = P(A) + P(B)
(c) P (A | B) = P(A ∩ B)/P(B)
(d) P(A ∪ B)< P(A) + P(B)
Answer/Explanation
Answer:(c) P (A | B) = P(A ∩ B)/P(B)
Explanation:
(a) P(A ∩ B) = P(A) P(B) is false since this is true if and only if A and B are independent events.
(b) P (A ∪ B) = P(A) + P(B) is false since P(A ∩ B) is zero if and only if A and B are mutually exclusive.
(c) P (A | B) = P(A ∩ B)/P(B) is true.
(d) P (A ∪ B) < P(A) + P(B) is false.
Since P(A ∪ B) ≤ P(A) + P(B)
Question 2.
A bag contains 10 white balls and 15 black balls. Two balls are drawn in succession. The probability that one of them is black and the other is white is
(a) \(\frac { 2 }{ 3 }\)
(b) \(\frac { 4 }{ 5 }\)
(c) \(\frac { 1 }{ 2 }\)
(d) \(\frac { 1 }{ 3 }\)
Answer/Explanation
Answer: (c) \(\frac { 1 }{ 2 }\)
Explanation:
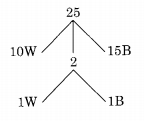
The bag contains 10 white balls and 15 black balls. Required probability
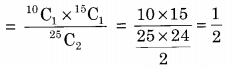
Question 3.
Two dice are thrown simultaneously. The probability that at least one of them will have 6 facing up is
(a) \(\frac { 1 }{ 36 }\)
(b) \(\frac { 1 }{ 3 }\)
(c) \(\frac { 25 }{ 36 }\)
(d) \(\frac { 11 }{ 36 }\)
Answer/Explanation
Answer:(d) \(\frac { 11 }{ 36 }\)
Explanation:
P(atleast one of dice will have 6 facing = 1 – P(none of dice have 6 facing up) = 1 – [\(\frac { 5 }{ 6 }\) × \(\frac { 5 }{ 6 }\)] = 1 – \(\frac { 25 }{ 36 }\) = \(\frac { 11 }{ 36 }\)
![]()
Question 4.
The probability that top and bottom cards of a randomly shuffled deck are both aces is
(a) \(\frac { 4 }{ 52 }\) x \(\frac { 4 }{ 52 }\)
(b) \(\frac { 4 }{ 52 }\) x \(\frac { 3 }{ 52 }\)
(c) \(\frac { 4 }{ 52 }\) x \(\frac { 3 }{ 51 }\)
(d) \(\frac { 4 }{ 52 }\) x \(\frac { 4 }{ 51 }\)
Answer/Explanation
Answer:(c) \(\frac { 4 }{ 52 }\) x \(\frac { 3 }{ 51 }\)
Explanation:
The probability that the bottom card of a randomly shuffled deck is ace = \(\frac { 4 }{ 52 }\) because there are 4 aces out of total 52 cards. From the remaining 3 aces out of 51 cards the probability that the top card is also an ace = \(\frac { 3 }{ 51 }\). So required probability = \(\frac { 4 }{ 52 }\) × \(\frac { 3 }{ 51 }\).
Question 5.
The probability that it will rain today is 0.5. The probability that it will rain tomorrow is 0.6. The probability that it will rain either today or tomorrow is 0.7. What is the probability that it will rain today and tomorrow?
(a) 0.3
(b) 0.25
(c) 0.35
(d) 0.4
Answer/Explanation
Answer:(d) 0.4
Explanation:
P(Rain today) = 0.5
P(Rain tomorrow) = 0.6
P(Rain today ∪ Rain tomorrow) = 0.7
P(Rain today ∩ Rain tomorrow) = ?
P(rain today ∩ Rain tomorrow) = P(Rain today) + P(rain tomorrow) – P(Rain today ∩ Rain tomorrow)
So; 0.7 = 0.5 + 0.6 – P(Rain today ∩ Rain tomorrow) P(Rain today ∩ Rain tomorrow) = 0.5+ 0.6-0.7 = 0.4
So, the probability that it will rain today and tomorrow is 0.4.
Question 6.
A die is rolled three times. The probability that exactly one odd number turns up among the three outcomes is
(a) \(\frac { 1 }{ 6 }\)
(b) \(\frac { 3 }{ 8 }\)
(c) \(\frac { 1 }{ 8 }\)
(d) \(\frac { 1 }{ 2 }\)
Answer/Explanation
Answer:(b) \(\frac { 3 }{ 8 }\)
Explanation:
Probability of getting an odd number in rolling of a die = \(\frac { 3 }{ 6 }\) = \(\frac { 1 }{ 2 }\). Now using binomial distribution P(Exactly one odd number among three outcomes)
= 3C1( \(\frac { 1 }{ 2 }\))1 ( \(\frac { 1 }{ 2 }\))2 = 3 × ( \(\frac { 1 }{ 2 }\))3 = ( \(\frac { 3 }{ 8 }\))
![]()
Question 7.
Suppose that the expectation of a random variable X is 5. Which of the following statements is true?
(a) There is a sample point at which X has the value 5.
(b) There is a sample point at which X has a value greater than 5.
(c) There is a sample point at which X has a value greater than or equal to 5.
(d) None of the above
Answer/Explanation
Answer:(c) There is a sample point at which X has a value greater than or equal to 5.
Explanation:
If all the points have X < 5, then the expectation of a random variable X is surely less than 5. So according to this, there should be at least a sample point at which X ≥ 5.
Question 8.
Consider two events E1 and E2 such that probability of E1 Pr [E1] = \(\frac { 1 }{ 2 }\), probability of E2, Pr [E2] = \(\frac { 1 }{ 3 }\), and probability of E1 and E2, Pr[E1 and E2] = \(\frac { 1 }{ 5 }\) . Which of the following statements is/are true?
(a) Pr[E1 or E2] is \(\frac { 2 }{ 3 }\)
(b) Events E1 and E2 are independent
(c) Events E1 and E2 are not independent
(d) pr \(\left[\frac{\mathrm{E}_{1}}{\mathrm{E}_{2}}\right]\) = \(\frac { 4 }{ 5 }\)
Answer/Explanation
Answer:(c) Events E1 and E2 are not independent
Explanation:
P(E1)= \(\frac { 1 }{ 2 }\) , P(E2) = \(\frac { 1 }{ 3 }\) and P(E1 ∩ E2) = \(\frac { 1 }{ 5 }\)
(a) P(E1 or E2)
= P(E1) + P(E2) – P(E1 ∩ E2)
= \(\frac { 1 }{ 2 }\) + \(\frac { 1 }{ 3 }\) – \(\frac { 1 }{ 5 }\) = \(\frac { 19 }{ 30 }\)
However given in option (a) is \(\frac { 2 }{ 3 }\).
So option (a) is not true.
(b) For independent events P(E1 ∩ E2) = P(E1) P(E2)
Here, P(E1 ∩ E2) = \(\frac { 2 }{ 5 }\)
P(E1) P(E2) = \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 3 }\) = \(\frac { 1 }{ 6 }\)
So; (P E1 ∩ E2) ≠ P(E1) P(E2)
So events E1 and E2 are not independent. Option (b) is not true.
(c) Since E1 and E2 are not independent So option (c) is true.
(d) P(E1/E2) =\(\frac{\mathrm{P}\left(\mathrm{E}_{1} \cap \mathrm{E}_{2}\right)}{\mathrm{P}\left(\mathrm{E}_{2}\right)}\) = \(\frac { 3 }{ 5 }\) So option (d) P(E1/E2) = \(\frac { 4 }{ 5 }\) is false.
Question 9.
E1 and E2 are events in a probability space satisfying the following constraints:
- Pr(E1) = Pr(E2)
- Pr(E1 ∪ E2) = 1
- E1 and E2 are independent
The value of Pr(E1), the probability of the event E1, is
(a) 0
(b) \(\frac { 1 }{ 4 }\)
(c) \(\frac { 1 }{ 2 }\)
(d) 1
Answer/Explanation
Answer:(d) 1
Explanation:
Constraints are
(i) P(E1) = P(E2) = x
(ii) P(E1 ∪ E2) = 1
(iii) E1 and E2 are independent so
P(E1 ∩ E2) = P(E1) P(E2) = x × x = x2
NOW,
P(E1 ∪ E2) = P(E1)+P(E2) – P(E1 ∩ E2)
1 = x + x – x2
1 = 2x – x2
x2 – 2x + 1 = 0
(x – 1)2 = 0
x = 1
So; P(E1) = P(E2) = x = 1
![]()
Question 10.
Seven (distinct) car accidents occurred in a week. What is the probability that they all occurred on the same day?
(a) \(\frac{1}{7^{7}}\)
(b) \(\frac{1}{7^{6}}\)
(c) \(\frac{1}{2^{7}}\)
(d) \(\frac{7}{2^{7}}\)
Answer/Explanation
Answer:(b) \(\frac{1}{7^{6}}\)
Explanation:
Sample space = 77
All accidents on the same day = 7 ways (all on Monday, all on Tuesday…)
So, required probability = \(\frac{7}{7^{7}}\) = \(\frac{7}{7^{6}}\)
Question 11.
Four fair coins are tossed simultaneously. The probability that at least one head and one tail turn up is
(a) \(\frac { 1 }{ 16 }\)
(b) \(\frac { 1 }{ 8 }\)
(c) \(\frac { 7 }{ 8 }\)
(d) \(\frac { 15 }{ 16 }\)
Answer/Explanation
Answer:(c) \(\frac { 7 }{ 8 }\)
Explanation:
p(atleast one head and one tail)
= 1 – p(no head or no tail)
= 1 – [p(no head) + p(no tail) – p(no head and no tail)]
= 1 – [p (all tails) + p(all heads) – 0]
= 1 – [\(\left[\frac{1}{2^{4}}+\frac{1}{2^{4}}-0\right]\) = 1 – \(\frac { 2 }{ 16 }\) = 1 – \(\frac { 1 }{ 8 }\) = \(\frac { 7 }{ 8 }\).
Or
Alternate Method:
We need atleast one head (≥1H) and atleast one tail (≥ 1 T). First we satisfy ≥ 1H as follows.
1 H, 3T
2 H, 2 T
3H, 1 T
and 4 H, 0 T
now to satisfy the second condition of ≥ 1 T, we have to remove 4 H, 0 T.
So, the favorable cases are only 1 H, 2 H, and 3 H. The probability of this by binomial distribution formula is
= \(\frac{{ }^{4} C_{1}}{2^{4}}\) + \(\frac{{ }^{4} C_{2}}{2^{4}}\) + \(\frac{{ }^{4} C_{3}}{2^{4}}\)= \(\frac { 7 }{ 8 }\)
Question 12.
Let P(E) denote the probability of the event E. Given P(A) = 1, P(B) = 1/2, and A and B are independent, the values of P(A | B) and P(B | A) respectively are
(a) \(\frac { 1 }{ 4 }\) , \(\frac { 1 }{ 2 }\)
(b) \(\frac { 1 }{ 2 }\) , \(\frac { 1 }{ 4 }\)
(c) \(\frac { 1 }{ 2 }\) , 1
(d) 1 , \(\frac { 1 }{ 2 }\)
Answer/Explanation
Answer:(d) 1 , \(\frac { 1 }{ 2 }\)
Explanation:
Given, P(A) = 1
P(B) = \(\frac { 1 }{ 2 }\)
Since both events are independent
P(A|B) = P(A) = 1
P(B|A) = P(B) = \(\frac { 1 }{ 2 }\)
Question 13.
A program consists of two modules executed sequentially. Let f1(t) and f2(t) respectively denote the probability density functions of time taken to execute the two modules. The probability density function of the overall time taken to execute the program is given by
(a) f1(t) + f2(t)
(b) \(\int_{t}^{0}\) f1 (X) f2 (X)dX
(c) \(\int_{t}^{0}\) f1 (X) f2 (t – X)dX
(d) max {f1(t), f2(t)}
Answer/Explanation
Answer:(c) \(\int_{t}^{0}\) f1 (X) f2 (t – X)dX
Explanation:
Let the time taken for first and second modules be represented by x and y and total time = t.
∴ t = x + y is a random variable. Now the joint density function
g(t) = \(\int_{0}^{t}\)f(x,y)dx
= \(\int_{0}^{t}\)f (x, t – x)dx
= \(\int_{0}^{t}\)f1(x) f2(t – x)dx
which is also called as convolution of f1 and f2, abbreviated as f1 * f2.Correct answer is therefore, choice (c).
![]()
Question 14.
If a fair coin is tossed four times. What is the probability that two heads and two tails will result?
(a) \(\frac { 3 }{ 8 }\)
(b) \(\frac { 1 }{ 2 }\)
(c) \(\frac { 5 }{ 8 }\)
(d) \(\frac { 3 }{ 4 }\)
Answer/Explanation
Answer:(a) \(\frac { 3 }{ 8 }\)
Explanation:
Given, P(H) = \(\frac { 1 }{ 2 }\)
P(T) = \(\frac { 1 }{ 2 }\)
Apply Bernoulli’s formula for binomial distribution,
P(X = 2) = \({ }^{4} \mathrm{C}_{2}\)(1/2)2(1 – \(\frac { 1 }{ 2 }\))4 – 2
= \({ }^{4} \mathrm{C}_{2}\) ( \(\frac { 1 }{ 2 }\) )2 (1/2)2
= \(\frac{{ }^{4} \mathrm{C}_{2}}{2^{4}}\) = \(\frac { 6 }{ 16 }\) = \(\frac { 3 }{ 8 }\)
Question 15.
In a population of N families, 50% of the families have three children, 30% of the families have two children and the remaining families have one child. What is the probability that a randomly picked child belongs to a family with two children?
(a) \(\frac { 3 }{ 23 }\)
(b) \(\frac { 6 }{ 23 }\)
(c) \(\frac { 3 }{ 10 }\)
(d) \(\frac { 3 }{ 5 }\)
Answer/Explanation
Answer:(b) \(\frac { 6 }{ 23 }\)
Explanation:
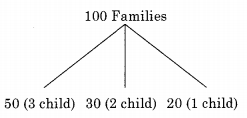
Total number of children = 50 × 3 + 30 × 2 + 20 × 1 = 230
Favorable cases = The number of children who come from 2 children families = 30 × 2 = 60
So the probability that a randomly picked child belongs to a 2 children families = \(\frac { 60 }{ 230 }\) = \(\frac { 6 }{ 23 }\)
Question 16.
Let X and Y be two exponentially distributed and independent random variables with mean a and β, respectively. If Z = min (X,Y), then the mean of Z is given by
(a) (1/(α + β))
(b) min (α, β)
(c) (αβ/(α + β))
(d) α + β
Answer/Explanation
Answer:(c) (αβ/(α + β))
Explanation:
f(x) = λ.e-λx, x ≥ 0
X and Y are two independent exponentially distributed random variables. Let λ1 and λ2 parameters of X and Y respectively.
P(X ≥ x)= e-λx, x > 0
P(Y ≥ x)=e-λ2x, x > 0
Given Z = min (X, Y)
P(Z ≥ x) = P(X ≥ x, Y ≥ x)
= P(X ≥ x) P(Y ≥ x)
= e-λ1x . e-λ2x = e-(λ1 + λ2)x
Since mean of exponential distribution = 1/Parameter
So, α = 1/λ1 ⇒ λ1 = 1/α
β = 1/λ2 ⇒ λ2 = 1/β
∴ Z is random variable with parameter
Mean of Z = IMG
Question 17.
An examination paper has 150 multiple-choice questions of one mark each, with each question having four choices. Each incorrect answer fetches — 0.25 mark. Suppose 1000 students choose all their answers randomly with uniform probability. The sum total of the expected marks obtained by all these students is
(a) 0
(b) 2550
(c) 7525
(d) 9375
Answer/Explanation
Answer:(d) 9375
Explanation:
Let the marks obtained per question be a random variable X. Its probability distribution table is given below:
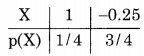
Expected marks per question = E(x)=ΣXP(X)
= 1 × \(\frac { 1 }{ 4 }\) + (-o.25) × \(\frac { 3 }{ 4 }\)
= \(\frac { 1 }{ 4 }\) – \(\frac { 3 }{ 16 }\) = \(\frac { 1 }{ 16 }\) marks
Total marks expected for 150 questions = \(\frac { 1 }{ 16 }\) × 150 = \(\frac { 75 }{ 8 }\) marks per student
Total expected marks of 1000 students = \(\frac { 75 }{ 8 }\) ×1000 =9375 marks
So correct answer is (d).
Question 18.
Two n bit binary strings, S1 and S2 are chosen randomly with uniform probability. The probability that the Hamming distance between these strings (the number of bit positions where the two strings differ) is equal to d is
(a) nCd/2n
(b) nCd/2d
(c) d/2n
(d) 1/2d
Answer/Explanation
Answer:(a) nCd/2n
Explanation:
If the hamming distance between two n bit strings is d, we are asking that d out of n trials be successful (success here means that the bits are different). So this is a binomial distribution with n trials and d successes and probability of success
P = \(\frac { 2 }{ 4 }\) = \(\frac { 1 }{ 2 }\)
(Since out of the 4 possibilities {(0,0), (0,1), (1, 0), (1,1)} only two of them (0,1) and (1,0) are success)
So p(X = d) = \({ }^{\mathrm{n}} \mathrm{C}_{\mathrm{d}}(1 / 2)^{\mathrm{d}}(1 / 2)^{\mathrm{n}-\mathrm{d}}\) = \(\frac{{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{d}}}{2^{\mathrm{n}}}\)
Correct choice is therefore (a).
![]()
Question 19.
A point is randomly selected with uniform probability in the X-Y. Plane within the rectangle with corners at (0, 0), (1, 0), (1, 2) and (0, 2). If p is the length of the position vector of the point, the expected value of p2 is
(a) \(\frac { 2 }{ 3 }\)
(b) 1
(c) \(\frac { 4 }{ 3 }\)
(d) \(\frac { 5 }{ 3 }\)
Answer/Explanation
Answer:
(d) \(\frac { 5 }{ 3 }\)
Explanation:
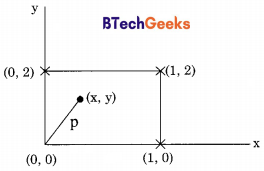
Length of position vector of point = p = \(\sqrt{x^{2}+y^{2}}\)
p2 = x2 + y2
E(p2) = E(x2 + y2) = E(x2) + E(y2)
Now x and y are uniformly distributes 0 ≤ x ≤ 1 and 0 ≤ y ≤ 2 Probability density function of x = \(\frac { 1 }{ 1 – 0 }\) = 1
The probability density function of

Question 20.
Let f(x) be the continuous probability density function of a random variable X. The probability that a < X ≤ b, is
(a) f (b – a)
(b) f(b) – f(a)
(c) \(\int_{b}^{a}\) f(X)dX
(d) \(\int_{b}^{a}\) xf (X)dX
Answer/Explanation
Answer:(c)\(\int_{b}^{a}\) f(X)dX
Explanation:
If f(x) is the continuous probability density function of a random variable X then, p(a < x ≤ b) = p(a ≤ x ≤ b) = \(\int_{b}^{a}\)f (x)dx
Question 21.
A bag contains 10 blue marbles, 20 green marbles and 30 red marbles. A marble is drawn from the bag, its colour recorded and it is put back in the bag. This process is repeated 3 times. The probability that no two of the marbles drawn have the same colour is
(a) \(\frac { 1 }{ 36 }\)
(b) \(\frac { 1 }{ 6 }\)
(c) \(\frac { 1 }{ 4 }\)
(d) \(\frac { 1 }{ 3 }\)
Answer/Explanation
Answer:
(b) \(\frac { 1 }{ 6 }\)
Explanation:
The given condition corresponds to sampling with replacement and with order. No 2 marbles have the same color i.e. Drawn 3 different marble. So total number of ways for picking 3 different marbles = 3! = 6. Probability of getting blue, green, red in order
= \(\frac { 10 }{ 60 }\) × \(\frac { 20 }{ 60 }\) × \(\frac { 30 }{ 60 }\) × 6
[Since 6 ways to get the marbles] = \(\frac { 1 }{ 6 }\)
Question 22.
An unbiased coin is tossed repeatedly until the outcome of two successive tosses is the same. Assuming that the trials are independent, the expected number of tosses is
(a) 3
(b) 4
(c) 5
(d) 6
Answer/Explanation
Answer:(a) 3
Explanation:
E(X) = S(Xi × Pi)
Where Xi = number of tosses until we get successive HEAD or TAIL.
Pi = Probability that we get in Xi tosses. Total possibilities by tossing a coin two times i.e. HT, HH, TH, TT. Out of which favorable cases are HH, TT.
P(X = 2) = \(\frac { 2 }{ 4 }\)
Similarly for X = 3 only THH and HTT are favorable out of a total of 8 outcomes.
So, P(X = 3) = \(\frac { 2 }{ 8 }\)
Similarly, we can see that in every case we will have only 2 favorable cases and 2n sample space.
So for nth toss probability = P(X = n) = 2/2n So the probability distribution table for X (the number of Tosses) is given below:
| X | 2 | 3 | 4 | 6 |
| P(X) | 2/4 | 2/8 | 2/16 | 2/32 |
E(X) = 2 × \(\frac { 2 }{ 4 }\) + 3 × \(\frac { 2 }{ 8 }\) + 4 × \(\frac { 2 }{ 16 }\) + …… It is combination of AP and GP form. So multiplying E(X) by \(\frac { 1 }{ 2 }\) and subtracting from E(X)
E(X) = 2 × \(\frac { 1 }{ 2 }\) + 3 × \(\frac { 1 }{ 4 }\) + 4 × \(\frac { 1 }{ 8 }\) + …..
\(\frac { 1 }{ 2 }\) × E(X) = 2 × \(\frac { 1 }{ 4 }\) + 3 × \(\frac { 1 }{ 8 }\) + 4 × \(\frac { 1 }{ 16 }\) + …..
After solving both equations we get,
\(\frac { 1 }{ 2 }\) × E(X) = 1 + \(\frac { 1 }{ 4 }\) + \(\frac { 1 }{ 8 }\) + \(\frac { 1 }{ 16 }\) + ……
\(\frac { 1 }{ 2 }\) × E(X) = 1 + \(\frac{1 / 4}{(1-1 / 2)}\) ⇒ E(X) = \(\frac { 6 }{ 4 }\) × 2 = 3
![]()
Question 23.
In a certain town, the probability that it will rain in the afternoon is known to be 0.6. Moreover, meteorological data indicates that if the temperature at noon is less than or equal to 25°C, the probability that it will rain in the afternoon is 0.4. The temperature at noon is equally likely to be above 25°C, or at/below 25°C.
What is the probability that it will rain in the afternoon on a day when the temperature at noon is above 25°C?
(a) 0.4
(b) 0.6
(c) 0.8
(d) 0.9
Answer/Explanation
Answer:(c) 0.8
Explanation:
Let RA : Rain in the afternoon T > 25: Temperature more than 25°C
Let the desired probability = P(RA | T ≤ 25) = x
The tree diagram for this problem is given below:
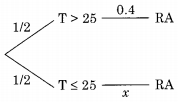
Given P(RA) = 0.6 by rule of total probability P(RA)
= \(\frac { 1 }{ 2 }\) × 0.4 + \(\frac { 1 }{ 2 }\) × x = 0.6 ⇒ x = 0.8
Question 24.
When a coin is tossed, the probability of getting a Head is p, 0 < p < 1. Let N be the random variable denoting the number of tosses till the first Head appears, including the toss where the Head appears. Assuming that successive tosses are independent, the expected value of N is
(a) 1/p
(b) 1/(1 – p)
(c) 1/P2
(d) 1/(1 – p2)
Answer/Explanation
Answer:(a) 1/p
Explanation:
The number of attempts to first succeed follows a geometric distribution. It is well known that the expected value in geometric distribution E(X) = 1/p. Where p is the probability of success in any one attempt.
Alternate Method:
Let X be the number of attempts to first success. Let p be the probability of success in any one attempt. Now the probability distribution table of X is given below:
| X | 1 | 2 | 3 | 4 |
| P(X) | p | (1 – p)p | (1 – p)2p | (1 – p)3p |
E(X) = Σ xp(x) = 1 × p + 2 × (p – 1) p + 3 × (p – 1)2 p + ……
This is the arithmetico-geometric series which can be solved as E(X) = 1/p
Question 25.
Suppose there are two coins. The first coin gives heads with probability \(\frac { 5 }{ 8 }\) when tossed, while the second coin gives heads with probability \(\frac { 1 }{ 4 }\). One of the two coins is picked up at random with equal probability and tossed. What is the probability of obtaining heads?
(a) \(\frac { 7 }{ 8 }\)
(b) \(\frac { 1 }{ 2 }\)
(c) \(\frac { 7 }{ 16 }\)
(d) \(\frac { 5 }{ 32 }\)
Answer/Explanation
Answer:(c) \(\frac { 7 }{ 16 }\)
Explanation:
The tree diagram for the problem is given below:
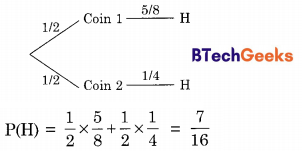
![]()
Question 26.
Suppose we uniformly and randomly select a permutation from the 20! permutations of 1, 2, 3,…, 20. What is the probability that 2 appears at an earlier position than any other even number in the selected permutation?
(a) \(\frac { 1 }{ 2 }\)
(b) \(\frac { 1 }{ 10 }\)
(c) \(\frac { 9! }{ 20! }\)
(d) None of these
Answer/Explanation
Answer:(d) None of these
Explanation:
The number of permutations with ‘2’ in the first position = 19!
The number of permutations with ‘2’ in the second position = 10 × 18!
(Fill the first space with any of the 10 add numbers and the 18 spaces after the 2 with 18 of the remaining numbers in 18! ways)
A number of permutations with ‘2’ in 3rd position = 10 × 9 × 17!
(Fill the first 2 places with 2 of the 10 odd numbers and then the remaining 17 places with the remaining 17 numbers) and so on until ‘2’ is in 11th place. After that, it is not possible to satisfy the given condition, since there are only 10 odd numbers available to fill before the ‘2’. So the desired number of permutations that satisfy the given condition is 19! + 10 × 18! + 10 × 9 × 17! + 10 × 9 × 8 × 16! + … + 10! × 9!
Now the probability of this happening is given by \(\frac{19 !+10 \times 18 !+10 \times 9 \times 17 ! \ldots+10 ! \times 9 !}{20 !}\)
which is clearly not choices (a), (b) or (c)
∴ Answer is (d) none of these.
Question 27.
In a multi-user operating system on average, 20 requests are made to use a particular resource per hour. The arrival of requests follows a Poisson distribution. The probability that either one, three, or five requests are made in 45 minutes is given by:
(a) 6.9 × 106 × e-20
(b) 1.02 × 106 × e-20
(c) 6.9 × 103 × e-20
(d) 1.02 × 103 × e-20
Answer/Explanation
Answer:(b) 1.02 × 106 × e-20
Explanation:
The requests follow poisson distribution with α = 20 requests/hr
The observation period = △T = 45 minutes = \(\frac { 45 }{ 60 }\) = \(\frac { 3 }{ 4 }\)hr
So the parameter for the poisson distribution = λ = α △ T= 20 × \(\frac { 3 }{ 4 }\) = 15
The required probability P(X = 1) + P(X = 3) + P(X = 5)
= \(\frac{e^{-15} 15^{1}}{1 !}\) + \(\frac{e^{-15} 15^{3}}{3 !}\) + \(\frac{e^{-15} 15^{5}}{5 !}\) = 1.02 × 106 × e-20
Question 28.
A sample space has two events A and B such that probabilities P(A ∩ B) = 1/2, P( \(\overline{\mathrm{A}}\) ) = 1/3, P( \(\overline{\mathrm{B}}\) ) = 1/3. What is P(A ∪ B)?
(a) \(\frac{11}{12}\)
(b) \(\frac{10}{12}\)
(c) \(\frac{ 9}{12}\)
(d) \(\frac{8}{12}\)
Answer/Explanation
Answer:(b) \(\frac{10}{12}\)
Explanation:
We know that:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
\(\overline{\mathrm{P}(\mathrm{A})}\) = 1 – P(A) and \(\overline{\mathrm{P}(\mathrm{B})}\) = 1 – P(B)
So, P(A) = ( 1 – \(\overline{\mathrm{P}(\mathrm{A})}\)) and P(B) = (1 – \(\overline{\mathrm{P}(\mathrm{B})}\))
P(A ∪ B) = (1 – \(\overline{\mathrm{P}(\mathrm{A})}\)) + (1 – \(\overline{\mathrm{P}(\mathrm{B})}\)) – P(A ∩ B)
= (1 – 1/3) + (1 – 1/3) – (1/2)
= (2/3) + (2/3) – (1/2)
= (4/3) – (1/2) = (5/6) = (10/12)
![]()
Question 29.
What is the probability that in a randomly chosen group of r people at least three people have the same birthday?

Answer/Explanation
Answer:
(c) 1 – \(\frac{365.364 \ldots(365-r+1)}{365^{r}}\) – rC2 . 365 . \(\frac{364.363 \ldots(364-(r-2)+1)}{364^{r-2}}\)
Explanation:
P(at least three people have the same birthday) = 1 – P (all have different b’days) – P(exactly two people have same b’day)
Now, P(all have different b’days) = \(\frac{365.364 \ldots(365-r+1)}{365^{r}}\)
P(exactly two people have same b’day) = \({ }^{r} C_{2} \cdot 365 \cdot \frac{364.363 \ldots(364-(r-2)+1)}{364^{r-2}}\)
[rC2 ways to choose who those two people with same b’day are, 365 ways to choose what the b’day is]
Now,
P (at least three people have the same birthday)
= 1 – \(\frac{365.364 \ldots(365-r+1)}{365^{r}}\)
= \({ }^{r} C_{2} \cdot 365 \cdot \frac{364.363 \ldots(364-(r-2)+1)}{364^{r-2}}\)
Which is option (c).
Question 30.
Aishwarya studies either computer science or mathematics every day. If she studies computer science on a day, then the probability that she studies mathematics the next day is 0.6. If she studies mathematics on a day, then the probability that she studies computer science the next day is 0.4. Given that Aishwarya studies computer science on Monday, what is the probability that she studies computer science on Wednesday?
(a) 0.24
(b) 0.36
(c) 0.4
(d) 0.6
Answer/Explanation
Answer:(c) 0.4
Explanation:
Let C denote computes science study and M denotes maths study. The tree diagram for the problem can be represented as shown below:
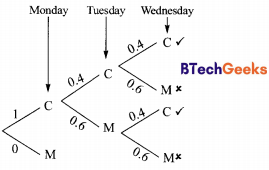
Now by the rule of total probability we total up the desired branches (✓) and get the answer as shown below:
p(C on Monday and C on Wednesday)
= p(C on Monday, C on Tuesday and C on Wednesday) + p(C on Monday, M on Tuesday, and C on Wednesday)
= 1 × 0.4 × 0.4 + 1 × 0.6 × 0.4 = 0.16 + 0.24 = 0.40
Question 31.
Let X be a random variable following a normal distribution with mean +1 and variance 4. Let Y be another normal variable with mean -1 and variance unknown. If P(X ≤ -1) = P(Y ≥ 2) the standard deviation of Y is
(a) 3
(b) 2
(c) \(\sqrt{2}\)
(d) 1
Answer/Explanation
Answer:(a) 3
Explanation:
Given µX = 1, σx2 = 4 => σx = 2 and µY = -1.σY is unknow
Given, p(X ≤ -1) = p(Y ≥ 2)
Converting into standard normal variates
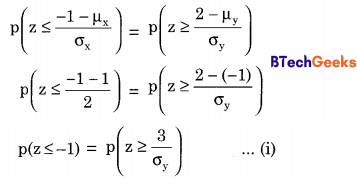
Now since we know that in a standard normal distribution,
p(z ≤ -1) = p(z ≥ 1) … (ii)
Comparing (i) and (ii) we can say that
\(\frac{3}{\sigma_{\mathrm{y}}}\) = 1 ⇒σy = 3
![]()
Question 32.
An unbalanced dice (with 6 faces, numbered from 1 to 6) is thrown. The probability that the face value is odd is 90% of the probability that the face value is even. The probability of getting any even-numbered face is the same. If the probability that the face is even given that it is greater than 3 is 0.75, which one of the following options is closest to the probability that the face value exceeds 3?
(a) 0.453
(b) 0.468
(c) 0.485
(d) 0.492
Answer/Explanation
Answer:(b) 0.468
Explanation:
It is given that, p(odd) = 0.9p(even)
Now since, Σp(x) = 1
∴ p(odd) + p (even) = 1
⇒ 0.9 p (even) + p (even) = 1
⇒ p(even) = \(\frac { 1 }{ 1.9 }\) = 0.5263
Now, it is given that p (any even face) is same i.e. p(2) = p(4) = p(6)
Now since,
p(even) = p(2) or p(4) or p(6)
= p(2) + p(4) + p(6)
∴ p(2) = p(4) = p(6)
= \(\frac { 1 }{ 3 }\) p (even) = \(\frac { 1 }{ 3 }\) (0.5263) = 0.1754
It is given that
p(even | face > 3) = 0.75
⇒ \(\frac{p(\text { even } \cap \text { face }>3)}{p(\text { face }>3)}\) = 0.75
⇒ \(\frac{\mathrm{p}(\text { face }=4,6)}{\mathrm{p}(\text { face }>3)}\) = 0.75
⇒ p (face>3) = \(\frac{p(\text { face }=4,6)}{0.75}\)
= \(\frac{p(4)+p(6)}{0.75}\)
= \(\frac{0.1754+0.1754}{0.75}\)
= 0.4677 ≃ 0.468
Question 33.
Consider a company that assembles computers. The probability of a faulty assembly of any computer is p. The company, therefore, subjects each computer to a testing process. This testing process gives the correct result for any computer with a probability of q. What is the probability of a computer being declared faulty?
(a) pq+(1 – p) (1 – q)
(b) (1 – q)p
(e) (1 – p)q
(d) pq
Answer/Explanation
Answer:(a) pq+(1 – p) (1 – q)
Explanation:
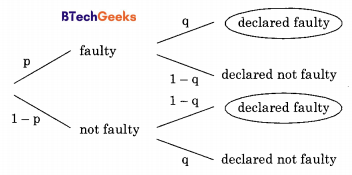
The tree diagram of probabilities is shown above. From above tree, by rule of total probability, p(declared faulty) = pq + (1 – p) (1 – q)
Question 34.
What is the probability that a divisor of 1099 is a multiple of 1096?
(a) \(\frac{1}{625}\)
(b) \(\frac{4}{625}\)
(c) \(\frac{12}{625}\)
(d) \(\frac{16}{625}\)
Answer/Explanation
Answer:(a) \(\frac{1}{625}\)
Explanation:
p(multiple of 1096 | divisor of 1099) = \(\frac{\mathrm{p}\left(\text { multiple of } 10^{96} \& \text { divisor of } 10^{99}\right)}{\mathrm{p}\left(\text { divisor of } 10^{99}\right)}\) = \(\frac{\mathrm{n}\left(\text { multiple of } 10^{96} \& \text { divisor of } 10^{99}\right)}{\mathrm{n}\left(\text { divisor of } 10^{99}\right)}\)
Since, 10 = 2 . 5
1099 = 299. 599
Any divisor of 1099 is of the form 2a . 5b where 0 ≤ a ≤ 99 and 0 ≤ b ≤ 99. The number of such divisors is given by (99+1) × (99 + 1) = 100 × 100.
So, no. of divisors of 10″ = 100 × 100.
Any number which is a multiple of 1096 as well as divisor of 1099 is of the form 2a. 5b where 96 ≤ a ≤ 99 and 96 ≤ b ≤ 99. The number of such combinations of 4 values of a and 4 values of b is 4 × 4 combinations, each of which will be a multiple of 1096 as well as a divisor of 1099.
∴ p(multiple of 1096 | divisor of 1099)
= \(\frac { 4 × 4 }{ 100 × 100 }\) = \(\frac { 1 }{ 625 }\)
Question 35.
If two fair coins are flipped and at least one of the outcomes is known to be ahead, what is the probability that both outcomes are heads?
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{2}{3}\)
Answer/Explanation
Answer:(a) \(\frac{1}{3}\)
Explanation:
Let A be the event of head in one coin. B be the event of head in second coin. The required probability is
P(A ∩ B | A ∪ B) = \(\frac { P{(A ∩ B) ∩ (A ∪ B)} }{ P(A ∪ B }\) = \(\frac { P(A ∩ B }{ P (A ∪ B)}\)
P( A ∩ B) = p(both coin heads) = p(H , H) = \(\frac { 1 }{ 4 }\)
P(A ∪ B) = p(at least one head)
p(HH, HT, TH) = \(\frac { 3 }{ 4 }\)
So required probability = \(\frac { 1/4 }{ 3/4 }\) = \(\frac { 1 }{ 3 }\)
![]()
Question 36.
If the difference between the expectation of the square of a random variable (E [x2] and the square of the expectation of the random variable (E [x])2 is denoted by R, then
(a) R = 0
(b) R < 0 (c) R ≥ 0 (d) R > 0
Answer/Explanation
Answer:
(c) R ≥ 0
Explanation:
V(x) = E(x2) – [E(x)]2 = R
where V(x) is the variance of x,
Since variance is σ2x and hence never negative, R ≥ 0.
Question 37.
Consider the finite sequence of random values X = [x1, x2,…, xn]. Let µx be the mean and σx be the standard deviation of X. Let another finite sequence Y of equal length be derived from this as yi = a * xn + b, where a and b are positive constants. Let µy be the mean and σy be the standard deviation of this sequence. Which one of the following statements INCORRECT?
(a) Index position of the mode of X in X is the same as the index position of the mode of Y in Y.
(b) Index position of the median of X in X is the same as the index position of the median of Y in Y
(c) µy = aµx + b
(d) σy = aσx + b
Answer/Explanation
Answer:
(d) σy = aσx + b
Explanation:
Standard deviation is affected by scale but not by the shift of origin.
So, yi = axi + b
⇒ σy = aσx
if a could be negative then σy = | a | σx is more correct since standard deviation cannot be negative)
Clearly, σy = aσx + b is false
So (d) is incorrect.
Question 38.
A deck of 5 cards (each carrying a distinct number from 1 to 5) is shuffled thoroughly. Two cards are then removed one at a time from the deck. What is the probability that the two cards are selected with the number on the first card being one higher than the number on the second card?
(a) \(\frac { 1 }{ 5 }\)
(b) \(\frac { 4 }{ 25 }\)
(c) \(\frac { 1 }{ 4 }\)
(d) \(\frac { 2 }{ 5 }\)
Answer/Explanation
Answer:
(a) \(\frac { 1 }{ 5 }\)
Explanation:
The five cards are {1, 2, 3, 4, 5}
Sample space = 5 × 4 ordered pairs.
[Since there is a Ist card and IInd card we have to take ordered pairs]
p(Ist card = IInd card + 1)
= P{(2, 1), (3, 2), (4, 3), (5, 4)} = \(\frac { 4 }{ 5 × 4 }\) = \(\frac { 1 }{ 5 }\)
Question 39.
Consider a random variable X that takes values +1 and -1 with probability 0.5 each. The values of the cumulative distribution function F(x) at x = -1 and +1 are (a) 0 and 0.5
(b) 0 and 1
(c) 0.5 and 1
(d) 0.25 and 0.75
Answer/Explanation
Answer:
(c) 0.5 and 1
Explanation:
The p.d.t of the random variable is
![]()
The cumulative distribution function F(x) is the probability up to x as given below:
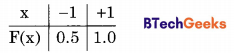
So the correct option is (c).
![]()
Question 40.
Suppose a fair six-sided die is rolled once. If the value on the die is 1, 2, or 3 then the die is rolled a second time. What is the probability that the sum total of values that turn up is at least 6?
(a) \(\frac { 10 }{ 21 }\)
(b) \(\frac { 5 }{ 12 }\)
(c) \(\frac { 2 }{ 3 }\)
(d) \(\frac { 1 }{ 6 }\)
Answer/Explanation
Answer:(b) \(\frac { 5 }{ 12 }\)
Explanation:
If first throw is 1, 2 or 3 then sample space is only 18 possible ordered pairs. Out of this only (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5) and (3, 6) i.e. 9 out of 18 ordered pairs gives a Sum ≥ 6.
If first throw is 4, 5 or 6 then second throw is not made and therefore the only way Sum ≥ 6 is if the throw was 6. Which is one out of 3 possible. So the tree diagram becomes as follows:
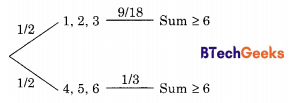
From above diagram
p(sum ≥ 6) = \(\frac { 1 }{ 2 }\) × \(\frac { 9 }{ 18 }\) + \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 3 }\) = \(\frac { 15 }{ 36 }\) = \(\frac { 5 }{ 2 }\)
Question 41.
Suppose p is the number of cars per minute passing through a certain road junction between 5 PM, and p has Poisson distribution with a mean 3. What is the probability of observing fewer than 3 cars during any given minute in this interval?
(a) 8/(2e3)
(b) 9/(2e3)
(c) 17/(2e3)
(d) 26/(2e3)
Answer/Explanation
Answer:
(c) 17/(2e3)
Explanation:
Poisson formula for (P = x) given as \(\frac{\mathrm{e}^{-\lambda} \lambda^{\mathrm{x}}}{\mathrm{x} !}\)
α = 3 cars/minute
△T = 1 minute
So λ = α △ T = 3 × 1 = 3
Probability of observing fewer than 3 cars = P(X < 3) = P(X ≤ 2)
= P(X = 0) + P(X = 1) + P(X = 2)
= \(\frac{\mathrm{e}^{-3} 3^{0}}{0 !}\) + \(\frac{\mathrm{e}^{-3} 3^{1}}{1 !}\) + \(\frac{e^{-3} 3^{2}}{2 !}\) = \(\frac{17}{2 \mathrm{e}^{3}}\)
Option (c) is correct.
Question 42.
Suppose you break a stick of unit length at a point chosen uniformly at random. Then the expected length of the shorter stick
is___________ .
Answer/Explanation
Answer:
Explanation:
Suppose you break a stick of unit length at a point chosen uniformly at random, then let the length of the shorter stick = x
x has uniform distribution in the interval [0,1/2] i.e. a = 0 and p – 1/2
In uniform distribution, E(x) = (β + α)/2
So the expected length of the shorter stick = E(x) = (1/2 + 0)/2 = 1/4 = 0.25
![]()
Question 43.
Four fair six-sided dice are rolled. The probability that the sum of the results being 22 is \(\frac { x }{ 1296 }\) The value of x is _________.
Answer/Explanation
Explanation:
Sample space = 64= 1296
6,6,6,4 ⇒ 4 ways (\(\frac { 4 ! }{ 3 !}\) = 4)
6,6,5,5 ⇒ 6 ways (\(\frac { 4 ! }{ 2!2!}\) = 6)
probability of sum to be 22 = \(\frac { 6 + 4 }{ 1296 }\) = \(\frac { x }{ 1296 }\)
⇒ x = 10</de
Question 44.
The security system at an IT office is composed of 10 computers of which exactly four are working. To check whether the system is functional, the officials inspect four of the computers picked at random (without replacement). The system is deemed functional if at least three of the four computers inspected are working. Let the probability that the system is deemed functional be denoted by p.
Then 100p = __________.
Answer/Explanation
Explanation:
The tree diagram for the problem is shown below.
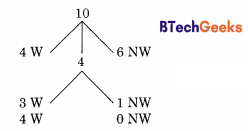
Required probability = \(\frac{{ }^{4} \mathrm{C}_{3} \cdot{ }^{6} \mathrm{C}_{1}}{{ }^{10} \mathrm{C}_{4}}\) + \(\frac{{ }^{4} \mathrm{C}_{3} \cdot{ }^{6} \mathrm{C}_{0}}{{ }^{10} \mathrm{C}_{4}}\) = \(\frac { 24 }{ 210}\)
+ \(\frac { 1 }{ 210 }\) = \(\frac { 25 }{ 210 }\)
p = 0.1190
⇒ 100 p = 11.90
Question 45.
The probability that a given positive integer lying between 1 and 100 (both inclusive) is NOT divisible by 2, 3 or 5 is _________.
Answer/Explanation
Explanation:
1 ≤ x ≤ 100
P(x is not divisible by 2, 3 or 5) = 1 – P(x is divisible by 2, 3 or 5)
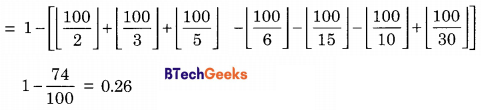
Question 46.
Let S be a sample space and two mutually exclusive events A and B be such that A ∪ B = S. If P(.) denotes the probability of the event, the maximum value of P(A) P(B) is ___________.
Answer/Explanation
Explanation:
It is given that A and B are mutually exclusive also it is given that A ∪ B = S which means that A and B are collectively exhaustive. Now if two events A and B are both mutually exclusive and collectively exhaustive, then P(A) + P(B) = 1 ⇒P(B) = 1-P(A)
Now we wish to maximize P(A) P(B) = P(A)(1-P(A))
Let, P(A) = x
Now P(A) (1 – P(A)) = x(1 – x) = x – x2
Say y = x- x2
\(\frac { dy }{ dx }\) = 1 – 2x = 0 ⇒ x = \(\frac { 1 }{ 2 }\)
= \(\frac { d^2y }{ dx^2 }\) = -2 < 0; (\(\frac { d^2y }{ dx^2 }\))x = \(\frac { 1 }{ 2 }\) = -2 < 0
y has maximum at x = \(\frac { 1 }{ 2 }\)
ymax = \(\frac { 1 }{ 2 }\) – (\(\frac { 1 }{ 2 }\))2 = 0.25
Question 47.
Suppose Xi for i = 1, 2, 3 are independent and identically distributed random variables whose probability mass functions are Pr[Xi = 0] = Pr[Xi = 1] = 1/2 for i = 1, 2, 3 Define another random variable Y=X1X2 ⊕ X3, where ⊕ denotes XOR. Then Pr[Y =0 |X3 = 0] =
Answer/Explanation
Explanation:
The p.d.t. for X1, X2, and X3 as given in the problem is shown below:
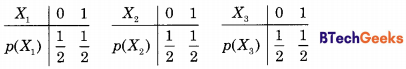
Given, Y = X1X2 ⊕ X3
The required probability – p(Y = 0 | X3 = 0)
= \(\frac{p\left(Y=0 \cap X_{3}=0\right)}{p\left(X_{3}=0\right)}\) …..(1)
Now, p{X3 = 0) = \(\frac { 1 }{ 2 }\) (from p.d.t. of X3) …(2)
p(Y = 0 ∩ X3 = 0)
= p (X1X2 ⊕ X3 = 0 ∩ X3 = 0)
= P((X1X2 ⊕ 0 ) = 0 ∩ X3 = 0)
= p(X1X2 = 0 ∩ X3 = 0)
= p(X1 = 0, X2 = 0, X3 = 0) + p(X1 = 0, X2 = 1, X3 = 0) + p(X1 = 1, X2 = 0, X3 = 0) + P(X1 = 1, X2 = 0, X3 = 0)
= \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 2 }\) = \(\frac { 3 }{ 8 }\)
So, p(Y = 0 ∩ X3 = 0) = \(\frac { 3 }{ 8 }\) ….(3)
Now substituting (2) and (3) in (1), we get
The required probability = p(Y = 0|X3 = 0) = \(\frac { 3/8 }{ 1/2 }\) = \(\frac { 3 }{ 4 }\) = 0.75
![]()
Question 48.
A probability density function on the interval [a, 1] is given by 1/x2 and outside this interval, the value of the function is zero. The value of a is ___________.
Answer/Explanation
Explanation:
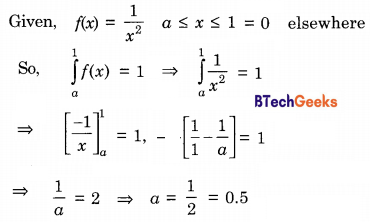
Question 49.
Consider the following experiment:
Step 1. Flip a fair coin twice.
Step 2. If the outcomes are (TAILS, HEADS) then output Yand stop.
Step 3. If the outcomes are either (HEADS, HEADS) or (HEADS, TAILS), then output Wand stop.
Step 4. If the outcomes are (TAILS, TAILS), then go to Step 1.
The probability that the output of the experiment is Y is __________(up to two decimal places)
Answer/Explanation
Explanation:
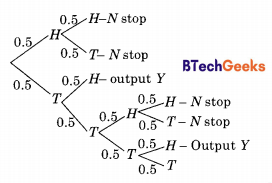
The tree diagram for the problem is given above. The desired output is Y. Now by rule of total probability P(output = Y) = 0.5 × 0.5 + 0.5 × 0.5 × 0.5 × 0.5 +… Infinite geometric series with α = 0.5 × 0.5 and r = 0.5 × 0.5 So p (output = Y)
= \(\frac { 0.5 × 0.5 }{ 1 -0.5 × 0.5 }\) = \(\frac { 0.25 }{ 0.75 }\) = \(\frac { 1 }{ 3 }\) = 0.33 (upto 2 decimal places)
Question 50.
Suppose that a shop has an equal number of LED bulbs of two different types. The probability of an LED bulb lasting more than 100 hours given that it is of Type 1 is 0.7, and given that it is of Type 2 is 0.4. The probability that an LED bulb is chosen uniformly at random lasts more than 100 hours is ___________.
Answer/Explanation
Explanation:

P(losts > 100 hr) = 0.5 × 0.7 + 0.5 × 0.4 = 0.35 + 0.2 = 0.55
Question 51.
Let X be a Gaussian random variable with mean 0 and variance σ2. Let Y = max (X, 0) where max (a, b) is the maximum of a and b. The median of Y is ___________.
Answer/Explanation
Explanation:
The Gaussian random variable is the same as the normal random variable.
So, the distribution of X is N(0, σ2)
For X, Median = Mean = Mode = 0 For Y = Max (X, 0)
Now half the data are below 0 and half the data above 0 for X. If we apply Y = Max(X, 0) now, all the negative values will become 0 and all the positive values will remain positive. So, the Median being positional average will not be affected and will remain at 0, since now half will be at 0 and a half will be positive. So, Median (Y) = 0.
Question 52.
P and Q are considering to apply for a job. The probability that P applies for the job is \(\frac { 1 }{ 4 }\) , the probability that P applies for the job given that Q applies for the job is \(\frac { 1 }{ 2 }\) , and the probability that Q applies for the job given that P applies for the job is \(\frac { 1 }{ 3 }\). Then the probability that P does 3 not apply for the job given that Q does not apply for the job is
(a) \(\frac { 4 }{ 5 }\)
(b) \(\frac { 5 }{ 6 }\)
(C) \(\frac { 7 }{ 8 }\)
(d) \(\frac { 11 }{ 12 }\)
Answer/Explanation
Answer:(a) \(\frac { 4 }{ 5 }\)
Explanation:
Given that,
p(P) = \(\frac { 1 }{ 4 }\) …..(1)
p(P | Q) = \(\frac { 1 }{ 2 }\) …..(2)
p(Q | p) = \(\frac { 1 }{ 3 }\) …..(3)
p(\(\bar{P}\) | \(\bar{Q}\) = ?
First solve for p(Q) and p (P ∩ Q) from equation (2) and (3) as follows:
From equation (2)
p(P | Q) = \(\frac { p(P ∩ Q) }{ P(Q) }\) = \(\frac { 1 }{ 2 }\) …(4)
From equation (3)
p(Q | P) = \(\frac { p(P ∩ Q) }{ P(P) }\) = \(\frac { 1 }{ 3 }\)
⇒ p(P ∩ Q) = \(\frac { 1 }{ 3 }\) × p(P) = \(\frac { 1 }{ 3 }\) × \(\frac { 1 }{ 4 }\) = \(\frac { 1 }{ 12 }\)
Now substitute in equation (4) and get
P(Q) = \(\frac { p(P ∩ Q) }{ 1/2 }\) = \(\frac { 1/12 }{ 1/2 }\) = \(\frac { 2 }{ 12 }\) = \(\frac { 1 }{ 6 }\)
So now we have p(P) = \(\frac { 1 }{ 4 }\)
p(Q) = \(\frac { 1 }{ 6 }\)
and p(P ∩ Q) = \(\frac { 1 }{ 12 }\) we need to find
p(\(\bar{P}\) | \(\bar{Q}\) = \(\frac{p(\bar{P} \cap \bar{Q})}{p(\bar{Q})}\)
= \(\frac{1-(P \cup Q)}{1-p(Q)}\) = 1 – \(\frac{[p(P)+p(Q)-p(P \cap Q)]}{1-p(Q)}\)
= \(\frac{1-\left[\frac{1}{4}+\frac{1}{6}-\frac{1}{12}\right]}{1-\frac{1}{6}}\) = \(\frac{\frac{2}{3}}{\frac{5}{6}}\) = \(\frac { 4 }{ 5 }\)
So, p(\(\bar{P}\) | \(\bar{Q}\) = \(\frac { 4 }{ 5 }\)
![]()
Question 53.
For any discrete random variable X, with probability mass function P(X = j) = pi, pj ≥ 0, j∈ {0,…, N}, and \(\sum_{j=0}^{N}\) pj = 1, define the polynomial function gx(z) = \(\sum_{j=0}^{N}\) PjZj For a certain discrete random variable Y, there exists a scalar β ∈ [0,1] such that gy (z) = (1- β + βz)N. The expectation of F is
(a) Nβ (1 – β)
(b) Nβ
(c) N (1 – β)
(d) Not expressible in terms of N and β alone
Answer/Explanation
Answer:(b) Nβ
Explanation:
gy(z) = ((1 – β) + βz)N
If gy(z) is expanded, we would get a bionomial distribution with n = N and p = β So the E(Y) = np = Nβ
Question 54.
If a random variable X has a Poisson distribution with mean 5, then the expectation E[(X + 2)2] equals __________.
Answer/Explanation
Explanation:
Given, Poisson distribution λ = 5 We know that in Poisson distribution E (X) = V(X) = λ
So here E(X) = V(X) = 5 Now, we need E[(X + 2)2]
= E(X2 +4X + 4)
= E(X2) + 4E(X) + 4
To find E(X2) we write, V(X) = E(X2) – (E(X))2
5 = E(X2) – 52 So, E(X2) = 52 + 5 = 30
Required value = 30+ 4 × 5 + 4 = 54
Question 55.
Two people, P, and Q, decide to independently roll two identical dice, each with 6 faces, numbered 1 to 6. The person with the lower number wins. In case of a tie, they roll the dice repeatedly until there is no tie. Define a trial as a throw of the dice by P and Q. Assume that all 6 numbers on each dice are equiprobable and that all trials are independent. The probability (rounded to 3 decimal places) that one of them wins on the third trial is ___________.
Answer/Explanation
Explanation:
P(one of them wins in 3rd trial)
= P(Ist trial is Tie) × P(IInd trial is Tie) × P(one of them wins 3rd trial)
P(Tie in any trial) = P(P = 1 and Q = 1) + P(P = 2 and Q = 2) + …. + P(P = 6 and Q = 6)
= \(\frac { 1 }{ 36 }\) + \(\frac { 1 }{ 36 }\) + \(\frac { 1 }{ 36 }\) + \(\frac { 1 }{ 36 }\) + \(\frac { 1 }{ 36 }\) +\(\frac { 1 }{ 36 }\) = \(\frac { 1 }{ 36 }\) = \(\frac { 1 }{ 6 }\)
P(one of them wins) = 1 = p(Tie) = 1 – \(\frac { 1 }{ 6 }\) = \(\frac { 5 }{ 6 }\)
So required probability = \(\frac { 1 }{ 6 }\) × \(\frac { 1 }{ 6 }\) × \(\frac { 5 }{ 6 }\) = \(\frac { 5 }{ 216 }\) = 0.023
(rounded to 3 decimal places)
![]()
Question 56.
Consider Guwahati (G) and Delhi (D) whose temperatures can be classified as high (H), medium (M), and low (L). Let P(HG) denote the probability that Guwahati has a high temperature. Similarly, P(MG) and P(LG) denotes the probability of Guwahati having medium and low temperatures respectively. Similarly, we use P(HD), P(MD), and P(LD) for Delhi. The following table gives the conditional probabilities for Delhi’s temperature given Guwahati’s temperature.
| HD | MD | LD | |
| HG | 0.40 | 0.48 | 0.12 |
| MG | 0.10 | 0.65 | 0.25 |
| LG | 0.01 | 0.50 | 0.49 |
Consider the first row in the table above. The first entry denotes that if Guwahati has high temperature (HG) then the probability of Delhi also having a high temperature (HD) is 0.40; i.e., P(HD | HG) = 0.40. Similarly, the next two entries are P(MD\HG) = 0.48 and P(LD | HG) = 0.12. Similarly for the other rows.
If it is known that P(HG) = 0.2, P(MG) = 0.5 and P(LG) = 0.3, then the probability (correct to two decimal places) that Guwahati has high temperature given that Delhi has high temperature is .
Answer/Explanation
Explanation:
The condition probability table given is
| HD | MD | LD | |
| HG | 0.40 | 0.48 | 0.12 |
| MG | 0.10 | 0.65 | 0.25 |
| LG | 0.01 | 0.50 | 0.49 |
P(HG) = 0.2, P(MG) = 0.5, P(LG) = 0.3 Drawing the tree diagram for HD we get,
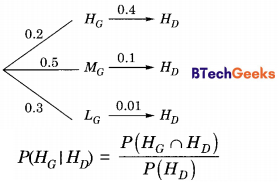
From diagram, P(HG ∩ HD) = 0.2 × 0.4
P(HD) = 0.2 × 0.4+ 0.5 × 0.1 + 0.3 × 0.01 = 0.133 Required probability,
P(HG | HD) = \(\frac { 0.2 × 0.4 }{ 0.133 }\) = 0.60 (rounding upto 2 decimal place)
Question 57.
Two numbers are chosen independently and uniformly at random from the set {1, 2, …, 13}. The probability (rounded off to 3 decimal places) that their 4-bit (unsigned) binary representations have the same most significant bit is ____________.
Answer/Explanation
Explanation:

p(2 elements out of 13 elements chosen randomly and independently) = (Number of MSB‘0’ × Number of MSB‘0’ + Number of MSB‘1’ × Number of MSB‘1’) / (Total × Total) = \(\frac{7 \times 7+6 \times 6}{13 \times 13}\) = \(\frac{49+36}{169}\) = \(\frac{85}{169}\) = 0.503
Question 58.
Suppose Y is distributed uniformly in the open interval (1,6). The probability that the polynomial 3x2 + 6xY+ 3Y+ 6 has only real roots is (rounded off to 1 decimal place) __________.
Answer/Explanation
Explanation:
polynomial 3x2 + 6xY + 3Y + 6 has only real roots
b2 – 4ax ≥ 0
(6Y)2 – 4(3) (3Y + 6) ≥ 0
Y2 – Y + 2 ≥ 0
Y ∈ (-∞, – 1] ∩ [2, ∞)
⇒ Y ∈ [2 , 6)
Since y is uniformly distributed in (1, 6) probability distributed function f(Y) = \(\frac { 1 }{ 5 }\) 1 p(2 ≤ y < 6) = \(\int_{2}^{6}\)f(Y)dy = \(\frac { 1 }{ 5 }\) \([Y]_{2}^{6}\) = \(\frac { 4 }{ 5 }\) = 0.8
Question 59.
For n > 2, let a e {0,1}n be a non-zero vector. Suppose that x is chosen uniformly at random from {0, 1}n. Then, the probability that \(\sum_{i=1}^{n}\)aixian odd number is _________.
Answer/Explanation
Explanation:

Fixed non-Zero
ai = 0 or 1
xi = 0 or 1
\(\sum_{i=1}^{n} a_{i} x_{i}\) value lies between 0 to n.
Total number cases = 2n
| Aixi | 0 | 1 | 2 | …………… | N |
| fav | nC0 | nC1 | nC2 | …………… | nCn |

Question 60.
Consider the two statements:
S1: There exist random variables X and Y such that(E[X-E(X)) (Y-E(Y))]2)>Var[X] Var[Y])
S2 : For all random variables X and Y Cov[X, Y] = E[| X-E[X] || Y-E[Y] |] Which one of the following choices is correct?
(a) Both S1 and S2 are false.
(b) Both S1 and S2 are true.
(c) S1 is true, but S2 is false.
(d) S1 is false, but S2 is true.
Answer/Explanation
Answer:
(a) Both S1 and S2 are false.
Explanation:
S2 : Cov(x,y) = E{|x – \(\bar{x}\)||y – \(\bar{y}\)|} is false
Case-I: If x > \(\bar{x}\) and y > \(\bar{y}\) then above is true.
Case-II: If x < \(\bar{x}\) and y < \(\bar{y}\) then above is true. Case-III: If x > \(\bar{x}\) but y < \(\bar{y}\) then above is false.
Case-IV: If x < \(\bar{x}\) but y > \(\bar{y}\) then above is false.
∵ Given expression is not always true. So we can conclude that it is false.
S1: It is obviously false,
∵ True statement is
[E{(x – \(\bar{x}\))(y – \(\bar{y}\))}]2 < var(x) . Var(y)
So both S1 and S2 are false.
Question 61.
The lifetime of a component of a certain type is a random variable whose probability density function is exponentially distributed with parameter 2. For a randomly picked component of this type, the probability that its lifetime exceeds the expected lifetime (rounded to 2 decimal places) is __________.
Answer/Explanation
Explanation:
Let, t = {lifetime of component} and μ = 2
Expected lifetime = \(\frac { 1 }{ μ }\)

Question 62.
A sender (S) transmits a signal, which can be one of the two kinds: H and L with probabilities 0.1 and 0.9 respectively, to a receiver (R). In the graph below, the weight of edge (u, v) is the probability of receiving v when u is transmitted, where u,v ∈ {H, L}. For example, the probability that the received signal is L given the transmitted signal was H, is 0.7.
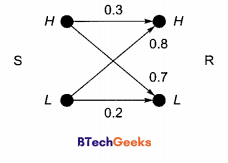
If the received signal is H, the probability that the transmitted signal was H (rounded to 2 decimal places) is .
Answer:
Explanation:
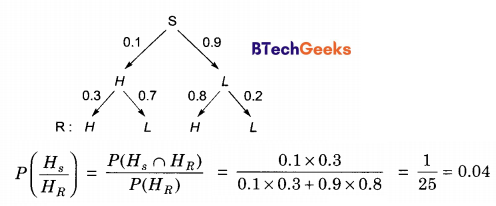
![]()
Question 63.
For a given biased coin, the probability that the outcome of a toss is ahead is 0.4. This coin is tossed 1,000 times. Let X denote the random variable whose value is the number of times that head appeared in these 1,000 tosses. The standard deviation of X (rounded to 2 decimal places) is ___________.
Answer/Explanation
Explanation:
n = 1000, p = 0.4, q = 0.6
It is a binomially distributed random variable.
So, S.D. = \(\sqrt{n p q}\)
= \(\sqrt{1000 \times 0.4 \times 0.6}\) = \(\sqrt{240}\) = 15.49
Question 64.
In an examination, a student can choose the order in which two questions (QuesA and QuesB) must be attempted.
- If the first question is answered wrong, the student gets zero marks.
- If the first question is answered correctly and the second question is not answered correctly, the student gets the marks only for the first question.
- If both the questions are answered correctly, the student gets the sum of the marks of the two questions.
The following table shows the probability of correctly answering a question and the marks of the question respectively.
| Question | Probability of answering correctly | Marks |
| QuesA | 0.8 | 10 |
| QuesB | 0.5 | 20 |
Assuming that the student always wants to maximize her expected marks in the examination, in which order should she attempt the questions, and what are the expected marks for that order (assume that the questions are independent)?
(a) First QuesA and then QuesB. Expected marks 14.
(b) First QuesB and then QuesA. Expected marks 22.
(c) First QuesB and then QuesA. Expected marks 14.
(d) First QuesA and then QuesB. Expected marks 16.
Answer/Explanation
Answer:
(d) First QuesA and then QuesB. Expected marks 16.
Explanation:
X → Random variable which represents total marks record.
P(X) → Probability of getting those marks.
| X → 0 | 10 | 20 | 30 |
| P(x) → 0.2 × 0.5 | 0.8 × 0.5 | 0.5 × 0.2 | 0.8 × 0.5 |
| 11 | 11 | 11 | 11 |
| 0.1 | 0.4 | 0.1 | 0.4 |
| ΣP(x) = 1 |
Now, if QuestionA is attempted first and it is correct.
Case-I:
E(x) = Σ(x) . P(x)
= 0.4 × 10 + 0.4 × 30 = 4 + 12 = 16
Case-II:
If QuestionB is attempted first and is correct.
E(x) – Σ(x) . P(x)
= 0.1 (20) + 0.4 (30)
= 2 + 12 = 14
So case-I is giving maximum expected marks. Hence option (d) is correct.
Question 65.
A bag has r red balls and b black balls. All balls are identical except for their colors. In a trial, a ball is randomly drawn from the bag, its color is noted and the ball is placed back into the bag along with another ball of the same color. Note that the number of balls in the bag will increase by one, after the trial. A sequence of four such trials is conducted. Which one of the following choices gives the probability of drawing a red ball in the fourth trial?

Answer/Explanation
Answer:
Explanation:
There are 10 favorable ways to calculate the probability of red ball in 4th trial.
(RFR)R = R or (BRR)R ≈ 1 way or (RRR)R ≈ 3 ways or (BBR)R ≈ 3 ways

