Computer Science Set Theory and Algebra MCQ Quiz Questions and Answers PDF Download
![]()
Question 1.
State whether the following statements are TRUE or FALSE:
The union of two equivalence relations is also an equivalence relation.
Answer/Explanation
Explanation:
A relation is said to be equivalence relation is
- Reflexive
- Symmetric, and
- Transitive
The union of two reflexive relations and two symmetric relations are reflexive and symmetric respectively. However, the union of two transitive relations need not be transitive. Therefore, the union of two equivalence relations need not be an equivalence relation.
Example:
Let R1 and R2 on set A = {1, 2, 3}
R1 = {(1, 1), (2, 2,), (3, 3) (1, 2), (2, 1)} is an equivalence relation
R2 = {(1, 1),(2, 2), (3, 3), (2, 3), (3, 2)} is an equivalence relation
R1 ∪ R2 = {(1, 1), (2, 2), (3, 3,), (1, 2), (2, 1), (2, 3), (3,2)} is not an equivalence relation, because (1, 2) & (2, 3) needs (1, 3) element to be in transitive relation.
Question 2.
(a) How many binary relations are there on a set A with n elements?
(b) How many one—to—one functions are there from a set A with n elements onto itself.
Answer/Explanation
Explanation: (a) Set A contains n elements. Every subset of A × A is a binary relation on set A.
∴ Number of binary relations on a set A with n elements 2n²
(b) Number of one-to-one functions from a set A with m-elements to a set B with n – elements are nPm So the number of one-to-one functions from a set A with n-elements to itself is nPn = n!.
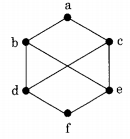
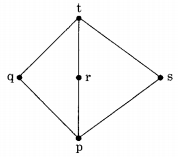
Question 3.
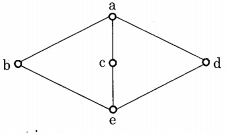
The complement(s) of the element ‘a’ in the lattice shown in the figure is (are)
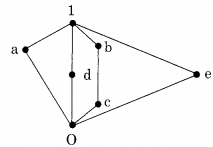
Answer/Explanation
Explanation: The complement of an element x is x’ iff LUB of x and x’ is 1 (greatest element) and GLB of x and x’ is 0 (least element).
∴ The complement of the element ‘a’ in the lattice = {b, c, d, e}.
Question 4.
The transitive closure of the relation {(1, 2) (2, 3) (3, 4) (5, 4)} on the set A = {1, 2, 3, 4, 5} is _______.
Answer/Explanation
Explanation:
The relation has (1, 2) (2, 3) then add (1, 3) to the relation. Since relation have (2, 3) (3,4) then add (2, 4) to relation.
So the resultant relation is = {(1, 2), (2, 3), (3, 4), (5, 4), (1, 3), (2, 4)} Now the resultant relation have (1,2) (2, 4) then add (1, 4) to the relation
∴ {(1,2), (2,3), (3,4), (5,4), (1,3), (2,4), (1,4)}
So the transitive closure of the relation is = {(1,2), (2,3), (3,4), (5,4), (1,3), (2,4), (1,4)}
Question 5.
Let S be an infinite set and S1, S2, … Sn sets such that S1 ∪ S2 ∪ ……. ∪ Sn = S. Then
(a) At least one of the sets Si is a finite set
(b) Not more than one of the sets Si can be finite
(c) At least one of sets Si is infinite
(d) Not more than one of the sets Si is an infinite set.
Answer/Explanation
Answer: (c) At least one of sets S; is infinite
Explanation:
S = S1 ∪ S2 ∪ S3 ∪ … ∪ Sn.
For S to be an infinite set, at least one of sets Si must be infinite, since if all Si were finite, then S will also be finite.
![]()
Question 6.
Let A be a finite set of size n. The number of elements in the power set of A × A is
(a) 22ⁿ
(b) 2n²
(c) 2n
(d) 2n
Answer/Explanation
Answer: (b) 2n²
Explanation:
Number of elements in A × A = n2
∴ A number of elements in the power set of A × A = 2n².
Question 7.
Some group (G, o) is known to be abelian. Then, which one of the following is true for G?
(a) g = g-1 for every g∈ G.
(b) g = g2 for every g ∈ G
(c) (goh)2 = g2 o h2 for every g, h ∈ G.
(d) G is of finite order
Answer/Explanation
Answer: (c) (goh)2 = g2 o h2 for every g, h ∈ G.
Explanation:
(goh)2 = (goh)o(goh)
Since group is abelian so it is commutative as well as associative.
= go (hog)h
= go (goh) oh
= (gog) o(hh) = g2 o h2
So (goh)2 = g2 o h2 for every g, h∈ G
Question 8.
Let R be asymmetric and transitive relation on a set A. Then
(a) R is reflexive and hence an equivalence relation
(b) R is reflexive and hence a partial order
(c) R is reflexive and hence not an equivalence relation
(d) None of the above
Answer/Explanation
Answer: (d) None of the above
Explanation:
A relation that is symmetric and transitive, need not be reflexive relation.
- R = { }; on the set A = {a, b}. The relation R is symmetric and transitive but not reflexive.
- R = {(a, a), (b, b)}; on the set A = {a, b}. The relation R is symmetric, transitive and also reflexive.
∴ A relation is transitive and symmetric relation but need not be reflexive relation.
Question 9.
The number of elements in the power set P(S) of the set S ={(Φ), 1, (2, 3)} is:
(a) 2
(b) 4
(c) 8
(d) None of these
Answer/Explanation
Answer: (c) 8
Explanation:
If a set has n elements then its powers set has 2n elements.
Given set S = {(Φ), 1, (2, 3)}
Number of elements in S = 3
∴ The number of elements in powerset (S)
= 23 = 8.
Question 10.
Let A be the set of all nonsingular matrices over real numbers and let * be the matrix multiplication operator. Then
(a) A is closed under * but <A, *> is not a semigroup.
(b) <A, *> is a semigroup but not a monoid.
(c) <A, *> is a monoid but not a group.
(d) <A, *> is a group but not an abelian group
Answer/Explanation
Answer: (d) <A, *> is a group but not an abelian group
Explanation:
- Closure Property: Multiplication of two non-singular matrices is also a non-singular matrix. Matrix multiplication over non-singular matrices follows closure properties.
- Associative Property: Multi-plication over any set of matrices is associative. (AB)C = A(BC) Where A, B, and C are non-singular matrices
- Identity Element: Identity matrix I am the identity element for matrix multiplication over matrices and I is non-singular.
- Inverse Element: For every non-singular matrix its inverse exists. So, for non¬singular matrices, inverse elements exist.
- Commutative: Matrix multiplication is not commutative
AB ≠ BA
Where A, B are non-singular matrices. Matrices multiplication is not commutative. So <A, *> is a group but not an abelian group
![]()
Question 11.
Let A and B set and let Ac and Bc denote the complements of the sets A and B. The set (A – B) ∪ (B – A) ∪ (A n B) is equal to
(a) A ∪ B
(b) Ac ∪ Bc
(c) A ∩ B
(d) Ac ∩ Bc
Answer/Explanation
Answer: (a) A ∪ B
Explanation:
(A – B) ∪ (B – A) ∪ (A ∩ B)
Representing the above set using the Venn diagram as follows.
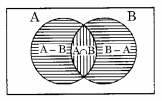
∴ By Venn diagram,
(A – B) ∪ (B – A) ∪ (A ∩ B) = A ∪ B
Question 12.
Let X = {2, 3, 6,12, 24}. Let ≤ be the partial order defined by x ≤ y if x divides y. The number of edges in the Hasse diagram of (X, ≤) is
(a) 3
(b) 4
(c) 9
(d) None of these
Answer/Explanation
Answer: (b) 4
Explanation:
x = {2, 3, 6, 12, 24}
The Hasse diagram of (x, ≤) is
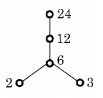
Therefore, the number of edges in the Hasse diagram = 4
Question 13.
Suppose X and Y are sets and |x| and |Y| are their respective cardinalities. It is given that there are exactly 97 functions from X to Y. From this one can conclude that
(a) |X| = 1, |Y| =97
(b) IXj =97, |Y| = 1
(c) j X | = 97, | Y | = 97
(d) None of the above
Answer/Explanation
Answer: (a) |X| = 1, |Y| =97
Explanation:
X and Y are set. The cardinalities of X and Y are |X| and |Y| respectively.
The number of functions from X to Y = (|Y|)|X| Given that number of functions from X to Y = 97
∴ 97 = (|Y|)|X|
So above implies that |X| = 1 and |Y| = 97
Question 14.
Which of the following statements is false?
(a) The set of rational numbers is an abelian group under addition
(b) The set of integers in an abelian group under addition
(c) The set of rational numbers form an abelian group under multiplication
(d) The set of real numbers excluding zero in an abelian group under multiplication
Answer/Explanation
Answer: (c) The set of rational numbers form an abelian group under multiplication
Explanation:
0 is also a rational number and for 0, the inverse doesn’t exist under multiplication. Therefore, the set of rational numbers doesn’t form an abelian group under multiplication.
![]()
Question 15.
Let R denote the set of real numbers. Let f:R x R → R x R be a bijective function defined by f(x, y) = (x + y, x – y). The inverse function of f is given by
(a) f-1(x,y) = \(\left(\frac{1}{x+y}, \frac{1}{x-y}\right)\)
(b) f-1(x,y) = (x – y, x + y)
(c) f-1(x,y) = \(\left(\frac{x+y}{2}, \frac{x-y}{2}\right)\)
(d) f-1(x,y) = (2(x – y), 2(x + y))
Answer/Explanation
Answer: (c) f-1(x,y) = \(\left(\frac{x+y}{2}, \frac{x-y}{2}\right)\)
Explanation:
f(x, y) = ((x + y), (x — y))
So let z1 = x+ y ……(i)
z2=x—y …(ii)
f(x, y) = (z1, z2)
So f-1(z1, z2) = (x, y)
Adding (i) and (ii)
z1 + z2 = 2x
X = \(\frac{\mathrm{z}_{1}+\mathrm{z}_{2}}{2}\)
Subtracting (i) and (ii)
z1 – z2 = 2y
y = \(\mathrm{y}=\frac{\mathrm{z}_{1}-\mathrm{z}_{2}}{2}\)
So the inverse function of F is given by
f-1(z1 , z2) = (x,y) = \(\left(\frac{\mathrm{z}_{1}+\mathrm{z}_{2}}{2}, \frac{\mathrm{z}_{1}-\mathrm{z}_{2}}{2}\right)\)
Since z1 and z2 are just dummy variables so replacing z1 and z2 by x and y respectively
f-1(x,y) = \(\left(\frac{x+y}{2}, \frac{x-y}{2}\right)\)
Alternate Method:
Given f(x, y) = ((x + y), (x — y))
Take some random ordered pair say (2, 3) f(2, 3) ((2 + 3), (2 — 3)) = (5, —1)
Now the correct inverse must map (5. —1) back to(2,3).
Trying the options one by one we find that only option (e) maps (5, -1) to (2, 3).
Question 16.
Let R be a non-empty relation on a collection of sets defined by ARB if and only if A ∩ B =Φ. Then, (pick the true statement)
(a) R is reflexive and transitive
(b) R is symmetric and not transitive
(c) R is an equivalence relation
(d) R is not reflexive and not symmetric
Answer/Explanation
Answer: (b) R is symmetric and not transitive
Explanation:
(i) Reflexive
A ∩ A = A ≠ Φ
So; (A, A) doesn’t belong to relation R.
∴ Relation R is not reflexive.
(ii) Symmetric
If A ∩ B = Φ then B ∩ A Φ is also true
∴ relation R is a symmetric relation.
(iii) Transitive
If A ∩ B = Φ and B ∩ C = Φ. it need not be true that A ∩ C = Φ.
For example:
A = {1, 2}, B = {3, 4}, C = {1, 5, 6}
A ∩ B = Φ and B ∩ C = Φ but
A ∩ C = {1} ≠ Ø
∴ Relation R is not transitive relation.
Question 17.
Which one of the following is false?
(a) The set of all bijective functions on a finite set forms a group under function composition.
(b) The set {1, 2, …, p – 1} forms a group under multiplication mod p where p is a prime number.
(c) The set of all strings over a finite alphabet Σ forms a group under concatenation.
(d) A subset s ≠ Φ of G is a subgroup of the group <G, *> if and only if for any pair of elements a, b ∈ s, a * b-1∈ s.
Answer/Explanation
Answer: (c) The set of all strings over a finite alphabet Σ forms a group under concatenation.
Explanation:
In option (c). the set of all strings over a finite alphabet Σ doesn’t form a group under concatenation because the inverse of a string doesn’t exist with respect to concatenation.
![]()
Question 18.
The number of equivalence relations on the set {1, 2, 3, 4} is
(a) 15
(b) 16
(c) 24
(d) 4
Answer/Explanation
Answer: (a) 15
Explanation:
Corresponding to every partition of the set 1, 2, 3, 4, there exists a unique equivalence relation. So we count every type of unordered partition of the set of 4 elements into one block, two-block, three-block, and four block partitions. as shown below:
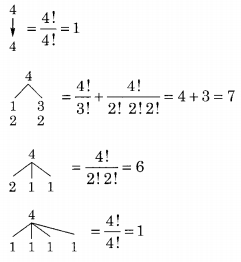
Total 1+7+6+1=15
So the number of equivalence relations on the set {1, 2, 3. 4} is 15.
Question 19.
Suppose A is a finite set with n elements. The number of elements in the Largest equivalence relation of A is
(a) n
(b) n2
(c) 1
(d) n + 1
Answer/Explanation
Answer: (b) n2
Explanation:
A is a finite set with n elements. The largest equivalence relation of A is the cross. product A × A and the number of elements in the cross product A × A is n2.
Question 20.
Let R1 and R2 be two equivalence relations on a set. Consider the following assertions:
(i) R1 ∪ R2 is an equivalence relation
(ii) R1 ∩ R2 is an equivalence relation
Which of the following is correct?
(a) both assertions are true
(b) assertion (i) is true but assertion (ii) is not true
(c) assertion (ii) is true but assertion (i) is not true
(d) neither (i) nor (ii) is true
Answer/Explanation
Answer: (c) assertion (ii) is true but assertion (i) is not true
Explanation:
A relation is said to be an equivalence relation if the relation is
(i) Reflexive
(ii) Symmetric
(iii) Transitive
Reflexive and symmetric properties are both closed under ∪ & ∩.
Transitive property is closed under n but not u. So equivalence relations are closed under ∩ hut not ∪.
Therefore R1 ∩ R2 is an equivalence relation but R1 ∪ R2 is not necessarily an equivalence relation.
![]()
Question 21.
The number of functions from an m element set to an n element set is
(a) m + n
(b) mn
(c) nm
(d) m * n
Answer/Explanation
Answer: (c) nm
Explanation:
The number of functions from an m element set to an n clement set is nm.
Question 22.
The binary relation R = {(1, 1), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4)} on the set A = {1, 2, 3, 4} is
(a) Reflexive, symmetric and transitive
(b) Neither reflexive, nor irreflexive but transitive
(c) Irreflexive, symmetric and transitive
(d) Irreflexive and antisymmetric
Answer/Explanation
Answer: (b) Neither reflexive nor irreflexive but transitive
Explanation:
The relation R doesn’t contain (4, 4), so R is not reflexive relation. Since relation R contains (1, 1), (2, 2), and (3, 3). Therefore, relation R is also not irreflexive.
That R is transitive, can be checked by systematically checking for all (a. b) and (b, c) in R, whether (a, e) also exists in R. So option (b) is correct.
Question 23.
Suppose A = {a, b, c, d} and Π1 is the following partition of A
Π1 = {{a, b, c}, {d}}
(a) List the ordered pairs of the equivalence relations induced by Π1
(b) Draw the graph of the above equivalence relation
Answer/Explanation
Answer: Given partition of A is
π1 = {(a, b, c), (d)}
(a) The ordered pairs of the equivalence relations induced by π1 is
R = (a, b, c) × (a, b, c) ∪ (d) × (d)
R = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c), (d, d)}
(b) The digraph of the above equivalence relation is as follows:
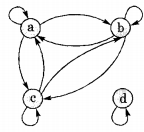
Question 24.
Let (A, *) be a semigroup. Furthermore, for every a and b in A, if a ≠ b, then a * b ≠ b * a.
(a) Show that for every an in A a * a = a
(b) Show that for every a, b in A a * b * a = a
(c) Show that for every a, b, c in A a * b * c = a * c
Answer/Explanation
Answer:
Explanation:
Given a ≠ b ⇒ a * b ≠ b * a The contrapositive version of this is a*b = b*a ⇒ a = b
(a) Now since (A, *) is given to be a semigroup, * is associative
i. e. a * (a * a) = (a * a) * a
Hence a = a * a
(b) (a * b * a) * a = a * b * (a * a) = a * b * a
⇒ a*(a*b*a) = (a*a)*b*a = a * b * a
as a * a = a [proved in part a]
So (a * b * a) * a = a * (a * b * a)
Hence a * b * a = a
(c) (a * b * c) * (a * c) = a * b * (c * a * c) = a * b * c
(a * c) * (a * b * c) = (a * c * a) * b * c = a * b * c
So (a *b * c) * (a * c) = (a * c) * (a * b * c)
Hence a*b*c = a*c
![]()
Question 25.
The number of binary relations on a set with n elements is
(a) n2
(b) 2n
(c) 2ⁿ²
(d) None of these
Answer/Explanation
Answer: (c) 2ⁿ²
Explanation:
The maximum number of elements in a binary relation on a set A with n elements = Number of elements in A × A = n2
Each element has two choices, either to appear on a binary relation or doesn’t appear on a binary relation.
∴ The number of binary relations = 2n².
Question 26.
(a) Mr. X claims the following:
If a relation R is both symmetric and transitive, then R is reflexive. For this, Mr. X offers the following proof. “From xRy, using symmetry we get yRx. Now because R is transitive, xRy and yRx together imply xRx. Therefore, R is reflexive.” Briefly point out the flaw in Mr. X’s proof.
(b) Give an example of a relation R which is symmetric and transitive but not reflexive.
Answer/Explanation
Explanation:
(a) According to Mr. X if xRy is in relation then yRx is also in relation because of symmetricity. Now because R is transitive, xRy and yRx implies xRx.
The flaw in Mr. X claim is that if xRy is present then only it implies yRx and hence xRx. However, if xRy is not present then according to symmetricity yRx is also not present. So xRx need not be present in relation. So it need not be reflexive.
For Example, Empty relation Φ is both symmetric and transitive. However, Φ is not reflexive relation.
(b) Examples of relations that are symmetric and transitive but not reflexive.
(i) Empty relation Φ is symmetric and transitive but not reflexive.
(ii) Relation R = {(a, b), (b, a), (a, a), (b, b)} over A = {a, b, c} is both symmetric and transitive but not reflexive.
Question 27.
A relation R is defined on the set of integers as xRy iff (x + y) is even. Which of the following statements is true?
(a) R is not an equivalence relation
(b) R is an equivalence relation having 1 equivalence class
(c) R is an equivalence relation having 2 equivalence classes
(d) R is an equivalence relation having 3 equivalence classes
Answer/Explanation
Answer: (c) R is an equivalence relation having 2 equivalence classes
Explanation:
A relation R is defined as xRy iff (x + y) is even over a set of integers.
(x + y) is even iff
(i) both x and y are even
(ii) both x and y are odd
Therefore, relation R is equivalence relation because relation is
(i) Reflexive
x + x = 2x = even
So (x, x) belongs to R. So relation is reflexive.
(ii) Symmetric
If x + y = even then y + x is also even So relation is symmetric.
(iii) Transitive
If x + y = even and y + z = even
Then x + y + y + z = even + even
⇒ x + z + 2y = even
⇒ x + z = even – 2y
⇒ x + z = even
∴ Relation R is transitive.
So relation R is an equivalence relation which divides the set of integer into two equivalence classes: One is of all even and other is of odd integer.
Equivalence classes of R are
[0] = { ….. -6, -4, -2, 0, 2, 4, 6, …}
[1] = { ….. -7, -5, -3, -1, 1, 3, 5, 7, …}
Question 28.
Let P(S) denote the power set of a set S. Which of the following is always true?
(a) P(P(S)) = P(S)
(b) P(S) ∩ P(P(S)) = {Ø}
(c) P(S) ∩ S = P(S)
(d) S ∉ P(S)
Answer/Explanation
Answer: (b) P(S) ∩ P(P(S)) = {Ø}
Explanation:
Φ always present in any powerset of a set and Φ is the only common element between P(S) and P(P(S))
∴ P(S) ∩ P(P(S)) = {Φ}
Question 29.
Consider the following relations
R1(a, b) iff (a + b) is even over the set of integers
R2(a, b) iff (a + b) is odd over the set of integers
R3(a, b) iff a.b > 0 over the set of non-zero rational numbers.
R4 (a, b) iff | a – b | ≤ 2 over the set of natural numbers
Which of the following statements is correct?
(a) R1 and R2 are equivalence relations, R3 and R4 are not
(b) R1 and R3 are equivalence relations, R2 and R4 are not
(c) R1 and R4 are equivalence relations, R2 and R3 are not
(d) R1, R2 R3, and R4 are all equivalence relations
Answer/Explanation
Answer: (b) R1 and R3 are equivalence relations, R2 and R4 are not
Explanation:
(I) Relation R1(a, b) iff (a + b) is even over the set of integers.
(i) a + a = 2a which is even So (a, a) belongs to R1
∴ R1 is reflexive relation
(ii) If (a + b) is even, then (b + a) is also even
∴ R1 is symmetric relation
(iii) If (a + b) and (b + c) are even then a + c = (a + b) + (b + c) – 2b = even + even — even = even
∴ R1 is transitive relation.
Since R1 is reflexive, symmetric and transitive so R1 is an equivalence relation.
(II) RR2(a, b) iff (a +b) is odd over set of integers,
(i) a + a = 2a which is not odd So (a, a) doesn’t belong to R2
∴ R2 is not reflexive relation Since R2 is not reflexive, it is not an equivalence relation.
(III) R3(a, b) iff a . b > 0 over set of non-zero relational numbers.
(i) a. a. > 0 for every non-zero rational number.
∴ R3 is reflexive relation.
(ii) If a.b > 0 then b.a > 0
∴ R3 is symmetric relation.
(iii) a.b > 0 and b.c > 0 ⇒ All a,b,c are positive or all a,b,c are negative.
So a.c > 0
∴ R3 is transitive relation.
So R3 is an equivalence relation.
(IV) R4 (a, b) iff |a – b| ≤ 2 over the set of natural number
(i) |a – a| ≤ 2
0 ≤ 2
∴ R4 is reflexive relation.
(ii) If |a — b| ≤ 2 then also |b – a| ≤ 2 ∴ R4 is symmetric relation
(iii) If |a — b| ≤ 2 and |b — c| ≤ 2 then it is not necessary that |a — c| ≤ 2
Ex. |3 – 5| ≤ 2 and |5 — 7| ≤ 2 but |3 —7| ≤ 2
∴ R4 is not transitive.
Since R4 is reflexive and symmetric not transitive, so R4 is not an equivalence relation.
Question 30.
Consider the following statements:
S1: There exist infinite sets A, B, C such that A ∩ (B ∩ C) is finite.
S2: There exist two irrational numbers x and y such that (x + y) is rational.
Which of the following is true about S1 and S2?
(a) Only S1 is correct
(b) Only S2 is correct
(c) Both S1 and S2 are correct
(d) None of S1 and S2 is correct
Answer/Explanation
Answer: (c) Both S1 and S2 are correct
Explanation:
S1: Let A = set of integers
B = set of odd integers
C = set of even integers
A ∩ (B ∩ C) = Φ and Φ is finite set.
Therefore, S1 is true.
S2: Let two irrational number x and y are respectively \((1+\sqrt{2})\) and \((1-\sqrt{2})\).
So x + y= 1 + \(\sqrt{2}\) +1 – \(\sqrt{2}\)
= 2 which is rational number Therefore, S2 is true. Since both S1 and S2 are true, option (c) is true.
![]()
Question 31.
Let f: A → B be a function and let E and F be subsets of A. Consider the following statements about images.
S1:f(E ∪ F)= f(E) ∪ f(F)
S2: f(E ∩ F) = f(E) ∩ f(F)
(a) Only S1 is correct
(b) Only S2 is correct
(c) Both S1 and S2 are correct
(d) None of S1 and S2 is correct
Answer/Explanation
Answer: (a) Only S1 is correct
Explanation:
Given a function f: x → y and subsets E and F of A then we have f(E ∪ F) = f(E) ∪ f(F) and f(E ∩ F) ⊆ f(E) ∩ f(F)
Therefore S1 is correct and S2 is false.
Question 32.
The binary relation S = f(empty set) on set A = {1, 2, 3} is
(a) Neither reflexive nor symmetric
(b) Symmetric and reflexive
(c) Transitive and reflexive
(d) Transitive and symmetric
Answer/Explanation
Answer: (d) Transitive and symmetric
Explanation:
The empty relation on any set is always transitive and symmetric but not reflexive.
Question 33.
Consider the set Σ* of all strings over the alphabet Σ = {0,1}. Σ* with the concatenation operator for strings
(a) does not form a group
(b) forms a non-commutative group
(c) does not have a right identity element
(d) forms a group if the empty string is removed from Σ*
Answer/Explanation
Answer: (a) does not form a group
Explanation:
Σ = {0, 1}
Σ* = {0,1}*
= {ε, 0, 1, 01, 10, 11, 000, …}
So (Σ*, •) is an algebraic system, where • (concatenation) is a binary operation.
So (Σ*, •) is a group if and only if the following conditions are satisfied.
1. • (Concatenation) is a closed operation.
2. • is an associative operation.
3. There is an identity.
4. Every element of Σ* has an inverse
Condition 1: * is a closed operation because for any ω1,∈ Σ* and ω2 ∈ Σ*, ω1 . ω2∈ Σ*
Condition 2: For any string x, y, z ∈ Σ*, x . (y . z) = (x . y) . z
So it is associative for example let
x = 01, y = 11, z = 00 then L.H.S. = x . (y.z)
= 01(1100) = 01(1100) = 011100 R.H.S. = (x.y).z
= (0111)00 = (0111)00 = 011100
Condition 3: The Identity is e or empty string because for any string ω ∈ Σ*,
εω = ωε = ω
Now, since ε ∈ Σ*, identity exists.
Condition 4: There is no inverse exist for Σ* because any string ω ∈ Σ*, there is no string ω-1 such that ω . ω-1 = ε = ω-1 ω.
So Σ* with the concatenation operator for strings doesn’t form a group but it does form a monoid.
Question 34.
Let (S, ≤) be a partial order with two minimal elements a and b, and a maximum element c. Let P: S →{True, False} be a predicate defined on S. Suppose that P(a) = True, P(b) = False and P(x) ⇒ P(y) for all x, y e S satisfying x ≤ y, where ⇒ stands for logical implication. Which of the following statements CANNOT be true?
(a) P(x) = True for all x ∈ S such that x ≠ b
(b) P(x) = False for all x ∈ S such that x ≠ a and x ≠ c
(c) P(x) = False for all x ∈ S such that b ≤ x such that x ≠ c
(d) P(x) = False for all x ∈ S such that a ≤ x and b ≤ x
Answer/Explanation
Answer: (d) P(x) = False for all x ∈ S such that a ≤ x and b ≤ x
Explanation:
If a ≤ x, since p(x) ⇒ p(y) whenever x ≤ y ∴ p(a) ⇒ p(x)
Now since p(a) = True, p(x) = cannot be false. ∴ (d) cannot be true.
![]()
Question 35.
Consider the set {a, b, c} with binary operators + and x defined as follows :
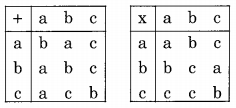
For example, a + c = c, c + a = a, c x b = c and b x c = a.
Given the following set of equations:
(a x x) + (a x y) = c
(b x x) + (c x y) = c
The number of solution (s) (i.e., pair (s) (x, y) that satisfies the equations) is
(a) 0
(b) 1
(c) 2
(d) 3
Answer/Explanation
Answer: (c) 2
Explanation:
The possible solution pairs are (a, a), (a, b), (a, e), (b, a), (b, b), (b, c), (c, a,), (c, b) and (e, c). Substitute them one by one in both equations and see which of them satisfies both the equations.
The given equations are:
(a × x)+(a × y) = C ……(i)
(b × x)+(c × y) = C ……(ii)
Substitute first (x. y) = (a, a)
LHS of equation (i) becomes (a × a) + (a × a) = a +a = b
Now RHS of equation (i) = e
Therefore LHS ≠ RHS. This means that (a, a) is not a solution pair. Similarly, try each of the remaining seven possible solution pairs. It will be found that only two pairs (b, c) and (c, b) will satisfy both equations (i) & (ii) simultaneously. Therefore choice (c) is correct.
Question 36.
Consider the binary relation:
S = {(x, y) | y = x + 1 and x, y e {0, 1, 2, ….}}
The reflexive transitive closure of S is
(a) {(x, y) | y > x and x, y ∈ {0, 1, 2, ….}}
(b) {(x, y) | y ≥ x and x,y ∈ {0, 1, 2, …..}}
(c) {(x, y) | y < x and x,y ∈ {0, 1, 2, ….}}
(d) {(x, y) | y ≤ x and x, y ∈ {0, 1, 2, ….}}
Answer/Explanation
Answer: (b) {(x, y) | y ≥ x and x,y ∈ {0, 1, 2, …..}}
Explanation:
S = {(x, y) | y = x + 1, and x, y ∈ (0, 1, 2, …}} = {(0, 1), (1, 2), (2, 3), (3, 4), …}
Now let T1 be the reflexive closure of S.
T1 = {(0, 0), (1, 1), (2, 2), (3, 3)…} ∪ {(0, 1), (1, 2), (2, 3), (3, 4)…}
= {(0, 0), (0, 1), (1, 1), (1, 2), (2, 2), (2, 3), (3, 3), (3, 4) …}
Let T2 be the transitive closure of S.
(0, 1), (1, 2) ∈ S ⇒ (0, 2) ∈ T2
(0, 2), (2, 3) ∈ S ⇒ (0, 3) ∈ T2
(0, 3), (3, 4) ∈ S ⇒ (0, 4) ∈ T2
and so on…..
Also (1, 2), (2, 3) ∈ S ⇒ (1, 3) ∈ T2
(1, 3), (3, 4) ∈ S ⇒ (1, 4) ∈ T2
(1, 4), (4, 5) ∈ S ⇒ (1, 5) ∈ T2
and so on….
∴ T2 = {(0, 1), (0, 2), (0, 3), …, (1, 2), (1, 3), (1, 4), …}
Now the reflexive, transitive closure of S will be T3 = T1 ∪ T2 = {(0, 0),(0, 1), (0, 2),…, (1,1), (1, 2), (1, 3),…,(2, 2) (2, 3), (2, 4),…}.
Option (b) is correct.
Question 37.
The number of different nxn symmetric matrices with each element being either 0 or 1 is: (Note : power (2, x) is same as 2x)
(a) power(2, n)
(b) power(2, n2)
(c) power(2, (n2 + n)/2)
(d) power (2, (n2 – n)/2)
Answer/Explanation
Answer: (c) power(2, (n2 + n)/2)
Explanation:
In a symmetric matrix, the lower triangle must be the mirror image of the upper triangle using the diagonal as a mirror. Diagonal elements may be anything. Therefore, when we are counting symmetric matrices we count how many ways are there to fill the upper triangle and diagonal elements. Since the first row has n elements, second (n -1) elements, third row (n – 2) elements, and so on up to the last row, one element.
Total number of elements in diagonal + upper triangle
= n + (n – 1) + (n – 2) + … + 1 = n(n + 1)/2
Now, each one of these elements can be either 0 or 1. So total number of ways we can fill these elements is
\(2 \frac{n(n+1)}{2}\) = power (2, (n2 + n)/2)
Since there is no choice for lower triangle elements the answer is power (2, (n2 + n)/2) which is choice (c).
Question 38.
In a class of 200 students, 125 students have taken Programming Language course, 85 students have taken Data Structures course, 65 students have taken Computer Organization course; 50 students have taken both Programming Language and Data Structures, 35 students have taken both Data Structures and Computer Organization; 30 students have taken both Data Structures and Computer Organization, 15 students have taken all the three courses. How many students have not taken any of the three courses?
(a) 15
(b) 20
(c) 25
(d) 30
Answer/Explanation
Answer: (c) 25
Explanation:
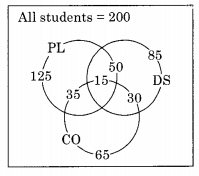
According to inclusion – exclusion formula:
| PL ∪ DS ∪ CO | = | PL | + | DS | + | CO | – | PL ∩ DS|- |PL – CO|-|DS ∩ CO| + |PL ∩ DS ∩ CO| PL = students who have taken programming. DS = Students who have taken Data structures. CO = Students who have taken Computer Organization.
So, the number of students who have taken atleast 1 of the 3 courses is given by:
= 125 + 85 + 65- 50- 35- 30 + 15 = 175
Therefore, the number of students who have not taken any of the 3 courses is = Total students – students taking at least 1 course = 200 – 175 = 25
![]()
Question 39.
Let R1 be a relation from A = {1, 3, 5, 7} to B= {2, 4, 6, 8} and R2 be another relation from B to C = {1, 2, 3, 4} as defined below:
(i) An element x in A is related to an element y in B (under R1) if x + y is divisible by 3.
(ii) An element x in B is related to an element y in C (under R2) if x + y is even but not divisible by 3.
Which is the composite relation R1R2 from A to C?
(a) R1R2={(1, 2), (1, 4), (3, 3), (5, 4), (7, 3)}
(b) R1R2={1, 2), (1, 3), (3, 2), (5, 2), (7, 3)}
(c) R1R2={1, 2), (3, 2), (3, 4), (5, 4), (7, 2)}
(d) R1R2={(3, 2), (3, 4), (5, 1), (5, 3), (7, 1)}
Answer/Explanation
Answer: (c) R1R2={1, 2), (3, 2), (3, 4), (5, 4), (7, 2)}
Explanation:
R1 = {(An element x in A, An element y in B) if x + y divisible by 3}
R1 = {(1, 2), (1, 8), (3, 6), (5, 4), (7, 2), (7, 8)}
R2 = {(An element x in B, An element y in C) if x + y is even but not divisible by 3}
R2 = {(2, 2), (4, 4), (6, 2), (6, 4), (8, 2)}
So, R1 o R2 = {(1, 2), (3, 2), (3, 4), (5, 4), (7, 2)}.
Question 40.
The following is the incomplete operation table of a 4-element group.
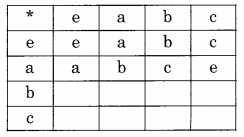
The last row of the table is
(a) c a e b
(b) c b a e
(c) c b e a
(d) c e a b
Answer/Explanation
Answer: (d) c e a b
Explanation:
Step 1:
By looking at the row for e, we see that it is a copy of the column headers. So e must be the identity element. Since right identity and left identity elements must both be the same. The column corresponding to e must be a copy of the row headers. We can now say that the operation table is:
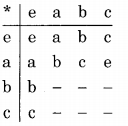
Step 2:
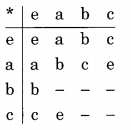
From the table above we see that a*c = e
∴ c*a must also be = e (if a is the inverse of c, then c is the inverse of a)
Now the operation table looks like
Step 3:
The blank in the second column must he c (since in a Cayley table, every row and every column is a unique permutation of the row and column headers).
Now the operation table looks like
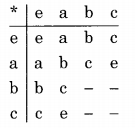
Step 4:
Now the blanks in the third row can be filled as a, e or e, a. Let us try each one in turn. If we fill a, e in the third row the operation table will look like
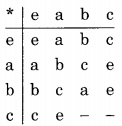
Now the blank in the fourth row and third column must be filled by e. However, this is not possible since e is already entered in the fourth row and second column. Therefore filling a, e in third-row blanks is wrong. So let us try filling the third-row blanks with e, a Now the operation table looks like
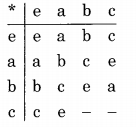
Now the blanks in the fourth row have to be filled with a, b The final operation table looks like
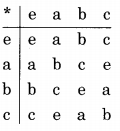
which is consistent with all the rules of a Cayley Table. The last row of this table is c, e, a, b Therefore the correct answer is (d).
Question 41.
The inclusion of which of the following sets into S = {{1, 2}, {1,2,3}, {1, 3, 5}, {1, 2, 4}, {1, 2, 3, 4, 5}} is necessary and sufficient to make S a complete lattice under the partial order defined by set containment?
(A) {1}
(b) {1}, {2, 3}
(c) {1}, {1, 3}
(d) {1}, (1, 3}, {1, 2, 3, 4}, {1, 2, 3, 5}
Answer/Explanation
Answer: (A) {1}
Explanation:
The hasse diagram of the given post is:
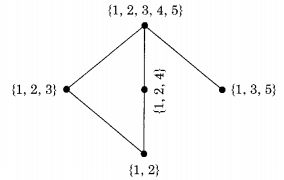
In a complete lattice L, every nonempty subset of L has both LUB and GLB. Now it is necessary to add {1} since GLB of {1,2} and {1, 3, 5} is {1}. The hasse diagram now becomes:
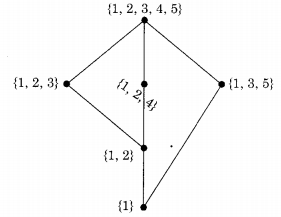
Now the above hasse diagram represents a complete lattice since every nonempty subset has both LUB and GLB. Therefore adding {1} is not only necessary but it is also sufficient to make the given lattice a complete lattice. Therefore the correct choice is (a).
Question 42.
Let A, B and C be non-empty sets and let X = (A – B) – C and Y = (A – C) – (B – C) Which one of the following is TRUE?
(a) X = Y
(b)X ⊂ Y
(c) Y ⊂ X
(d) None of these
Answer/Explanation
Answer: (a) X = Y
Explanation:
X = (A-B) – C
= (A ∩ B’) – C
= (A ∩ B’) ∩ C’
= AB’C’
Y= (A-C)-(B-C)
= (A ∩ C) – (B ∩ C’)
= (AC’) – (BC’)
= (AC’) ∩ (BC’)’
= (AC’) ∩ (B’ + C)
= (AC’) . (B’ + C)
= AC’B’ + AC’C
= AC’B’ (Since C’C = 0)
= AB’C’ (commutative property)
∴ X =Y
![]()
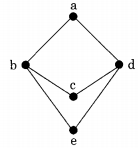
Question 43.
The following is the Hasse diagram of the poset [{a, b, c, d,e}, ≤]
The poset is
(a) not a lattice
(b) a lattice but not a distributive lattice
(c) a distributive lattice but not a Boolean algebra
(d) a Boolean algebra
Answer/Explanation
Answer:(b) a lattice but not a distributive lattice
Explanation:
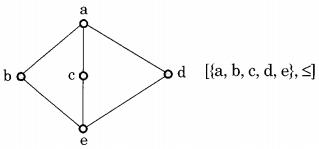
The poset [{a, b, c, d, e}, ≤ ] is a lattice (since every pair of elements has LUB and GLB) but it is not a distributive lattice. Because distributive lattice satisfies the following conditions. For any x, y, z,
x ∧ (y v z) — (x ∧ y) v (x ∧ z)
x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z)
Where ∧ and ∨ are meet and join operations but for given poset [{a, b, c, d, e} ≤]
b ∧ (c ∨ d) = b ∧ a = b
(b ∧ c) ∨ (b ∧ d) = e ∨ e = e
So it is not distributive. (Also, element b has 2 complements c and d, which is not possible in a distributive lattice, since, in a distributive lattice, complement if it exists, is always unique).
Question 44.
The set {1, 2, 4, 7, 8,11,13,14} is a group under multiplication modulo 15. The inverses of 4 and 7 are respectively
(a) 3 and 13
(b) 2 and 11
(c) 4 and 13
(d) 8 and 14
Answer/Explanation
Answer: (c) 4 and 13
Explanation:
The set S = {1, 2, 4, 7, 8, 11, 13, 14} is a group under multiplication modulo 15.
The identity element for this group is e = 1 since,
∀x ∈ S, 1 . x mod 15 = x
Now let the inverse of 4 be 4-1.
Now (4 . 4-1) mod 15 = e = 1
Since (4 . 4) mod 15=1
∴ 4-1 = 4 (This inverse is unique)
Similarly let the inverse of 7 be 7-1
(7 . 7-1) mod 15=1
putting each element of set as 7-1 by trial and error we get
(7 . 13) mod 15 = 91 mod 15=1
∴ 7-1 = 13
So, 4-1 and 7-1 are respectively 4 and 13. The correct choice is (c).
Question 45.
Let R and S be any two equivalence relations on a non-empty set A. Which one of the following statements is TRUE?
(a) R ∩ S, R ∪ S are both equivalence relations
(b) R ∪ S is an equivalence relation
(c) R ∩ S is an equivalence relation
(d) Neither R ∪ S nor R ∩ S is an equivalence relation
Answer/Explanation
Answer: (c) R ∩ S is an equivalence relation
Explanation:
R ∩ S is an equivalence relation as can be seen from proof given below.
Let ∀x ∈ A (x, x) ∈ R and (x, x) ∈ S (since R and S are reflexive)
∴ (x, x) ∈ R n S also ∴ R ∩ S is reflexive.
Now, (x, y) ∈ R ∩ S
⇒ (x, y) ∈ R and (x, y) ∈ S
⇒ (y, x) ∈ R and (y, x) ∈ S
(Since R and S are symmetric)
⇒ (y,x) ∈ R ∩ S
∴ (x, y) ∈ R ∩ S
⇒ (y, x) ∈ R ∩ S
R ∩ S is therefore symmetric Now consider
(x, y) and (y, z) ∈ R ∩ S ⇒ (x, y) and (y, z) ∈ R and (x, y) and (y, z) ∈ S ⇒ (x, z) ∈ R and (x, z) ∈ S
(Since R and S are transitive)
⇒ (x, z) ∈ R ∩ S
∴ R ∩ S is transitive also. Since R ∩ S is reflexive, symmetric, and transitive.
∴ R ∩ S is an equivalence relation.
Note: A similar argument cannot be made from R ∪ S.
Question 46.
Let f: B → C and g: A → B be two functions and let h = f o g. Given that h is an onto function. Which one of the following is TRUE?
(a) f and g should both be onto functions
(b) f should be onto but g need not be onto
(c) g should be onto but f not be onto
(d) both f and g need not be onto
Answer/Explanation
Answer: (b) f should be onto but g need not be onto
Explanation:
Consider the arrow diagram shown below:
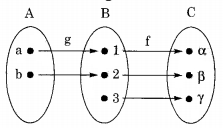
h(a) = f . g(a) = α
h(b) = f . g(b) = β
Here f is onto but g is not onto, yet h is onto. As can be seen from the diagram if f is not onto, h cannot be onto.
∴ f should be onto, but g need not be onto.
∴ The answer is (b).
![]()
Question 47.
Consider the set H of all 3 × 3 matrices of the type
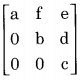
where a, b, c, d, e, and f are real numbers and abc ≠ 0. Under the matrix multiplication operation, the set H is
(a) a group
(b) a monoid but not a group
(c) a semigroup but not a monoid
(d) neither a group nor a semigroup
Answer/Explanation
Answer: (a) a group
Explanation:
(i) The set H is closed since the multiplication of upper triangular matrices will result only in the upper triangular matrix.
(ii) Matrix multiplication is associative, i.e.
A * (B * C) = (A * B) * C.
(iii) Identity element is
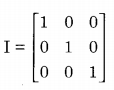
and this belongs to H as I is an upper triangular as well as a lower triangular matrix.
(iv) If A ∈ H, then | A | = abc. Since it is given that abc ≠ 0, this means that |A | ≠ 0 i.e. every matrix belonging to H is non-singular and has a unique inverse.
∴ the set H along with matrix multiplication is a group.
Question 48.
Let f be a function from a set A to a set B, g a function from B to C, and h a function from A to C, such that h(a) = g(f(a)) for all an ∈ A. Which of the following statements is always true for all such functions f and g?
(a) g is onto ⇒ h is onto
(b) h is onto ⇒ f is onto
(c) h is onto ⇒ g is onto
(d) h is onto ⇒ f and g are onto
Answer/Explanation
Answer: (c) h is onto ⇒ g is onto
Explanation:
Given, h = g(f(x)) = g.f
Consider the following arrow diagram:
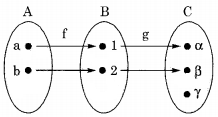
From the above diagram it is clear that g is not onto ⇒ h = g.f is also not onto, since the co-domain of g is the same as the co-domain of g.f. The contrapositive version of the above implication is h is onto ⇒ g is onto which also has to be true since direct = contrapositive. So option (c) is true.
Question 49.
Let A be a set with n elements. Let C be a collection of distinct subsets of A such that for any two subsets S1 and S2 in C, either S1 ⊂ S2 or S2 ⊂ S1 What is the maximum cardinality of C?
(a) n
(b) n+1
(c) 2n-1 +1
(d) n!
Answer/Explanation
Answer: (b) n+1
Explanation:
The way C is defined in the question contains only comparable subsets of A. i.e. the set C is the set of all comparable subsets of set A. Such a set is called a chain. Consider an example with set A = {1, 2} Subsets are Φ, {1}, {2} and {1, 2} Maximum cardinality of collection of distinct subsets is {Φ, {1} and {1, 2}} i.e. 3. So with n elements, the maximum cardinality is n + 1.
![]()
Question 50.
For the set N of natural numbers and a binary operation f: N × N → N, an element z ∈ N is called an identity for f, if f(a, z) = a = f(z, a), for all an e N. Which of the following binary operations have an identity?
I. f(x, y) = x + y – 3
II. f(x, y) = max(x, y)
III. f(x, y) = xy
(a) I and II only
(b) II and III only
(c) I and III only
(d) None of these
Answer/Explanation
Answer: (d) None of these
Explanation:
I. f(x) = x + y – 3
x + a – 3 = x = a + x – 3
so a = 3
Now 3 is unique, and 3 ∈ N So I has identity.
II: f(x) = max(x, y)
max(x, a) = x = max(a, x)
In N, the only value of a which will satisfy the above equation is a = 1.
Since 3 is unique, and 3 ∈ N So II has an identity.
III. f(x) = xy
xa = x = ax
Now xa = x ⇒ a = 1, but x= ax has no solution for a in the set N.
So III has no identity.
So only I and II have an identity.
Question 51.
Let, X, Y, Z be sets of sizes x, y, and z respectively. Let W = X × Y and E be the set of all subsets of W. The number of functions from Z to E is
(a) z
(b) 2 × 2xy
(c) 2z
(d) 2xyz
Answer/Explanation
Answer: (d) 2xyz
Explanation:
Given | X | = x, | Y | = y and | Z | = z W = X × Y
So | W| = xy
| E | = 2|W| =2xy
So the number of functions for Z to E = | E | |z|
= (2xy)z = 2xyz
Question 52.
The set {1, 2, 3, 5, 7, 8, 9} under multiplication modulo 10 is not a group. Given below are four possible reasons. Which one of them is false?
(a) It is not closed
(b) 2 does not have an inverse
(c) 3 does not have an inverse
(d) 8 does not have an inverse
Answer/Explanation
Answer: (c) 3 does not have an inverse
Explanation:
Let A = {1, 2, 3, 5, 7, 8, 9}
Construct the table for any x, y ∈ A such that x * y = (x.y) mod 10
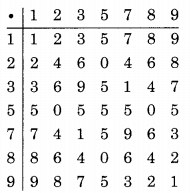
We know that 0 ∉ A. So it is not closed. Therefore, (a) is true.
The identity element = 1
∴ (2 . 2-1) mod 10 = 1
From the table, we see that 2-1does not exist. Since, (3 . 7) mod 10 = 1
∴ 7 is the inverse of 3 and 7 ∈ A.
(c) is false.
(d) is true since 8 does not have an inverse.
Question 53.
A relation R is defined on ordered pairs of integers as follows: (x, y)R(u,v) if x < u and y > v. Then R is
(a) Neither a Partial Order nor an Equivalence Relation
(b) A Partial Order but not a Total Order
(c) A Total Order
(d) An Equivalence Relation
Answer/Explanation
Answer: (a) Neither a Partial Order nor an Equivalence Relation
Explanation:
(x, y) R (u, v) iff x < u and y > v
(x, x) (x, x) since x / x and x / x
So R is not reflexive,
∴ R is neither a partial order, nor an equivalence relation.
Question 54.
Let E, F and G be finite sets:
Let X = (E ∩ F) – (F ∩ G) and Y = (E – (E ∩ G)) – (E – F).
Which one of the following is true?
(a) X ⊂ Y
(b) X ⊃ Y
(c) X = Y
(d) X – Y ≠ Ø and Y – X ≠ Ø
Answer/Explanation
Answer: (c) X = Y
Explanation:
Consider the following Venn diagram for X = (E ∩ F) – (F ∩ G)
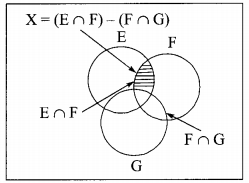
Y = (E -(E ∩ G)) – (F – F)
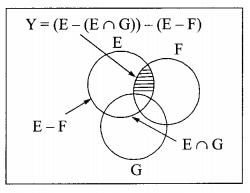
So, X = Y
or alternatively the solution can be obtained from boolean algebra as follows:
X = (E ∩ F) – (F ∩ G)
= EF – FG
= EF ∩ (FG)’
= EF . (F’ + G’)
= EFF’ + EFG’
= EFG’
Similarly, Y = (E -(E ∩ G)) – (E – F)
= (E – EG) – (E . F’)
= E . (EG)’ – EF’
= E . (E’ + G’) – EF’
= EG’ – EF’
= EG’ . (EF’)’
= EG’ . (E’ + F)
= EE’ G’ + EFG’
= EFG’
Therefore X = Y
![]()
Question 55.
Let S = {1, 2, 3,…, m}, m > 3. Let X1, X2,…, Xn be subsets of S each of size 3. Define a function f from S to the set of natural numbers as, f(i) is the number of sets Xj that contains the element i. That is f(i) = | {j | i∈ Xj} |.
Then \(\sum_{i=1}^{m}\) (i) is
(a) 3m
(b) 3n
(c) 2m +1
(d) 2n + 1
Answer/Explanation
Answer: (b) 3n
Explanation:
The problem can be solved by considering the cases m = 4 and m = 5 etc.
Let, m = 4
S = {1, 2, 3, 4}
n = number of 3 element subsets
= 4C3 = 4C1 = 4
n = 4
The 4 subsets are {1, 2, 3}, {1, 2, 4}, {1, 3, 4} and {2, 3, 4}
f(1) = number of subsets having 1 as an element = 3
f(2) = number of subsets having 2 as an element = 3
f(3) = 3 and f(4) = 3
∴ \(\sum_{i=1}^{4} f(i)\) = 3 + 3 + 3 + 3=12
Both choice (a) and choice (b) are matching the answer since
3m = 3n = 12
Now let us try m = 5
S = {1, 2, 3, 4, 5}
n = number of 3 element subsets = 5C3 = 10
∴ n = 10
The 10 subsets are {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, {2, 4, 5}, {3, 4, 5}
f(1) = f(2) = f(3) = f(4) = f(5) = 6
\(\sum_{i=1}^{5} f(i)\) = 6 + 6 + 6 + 6 + 6 = 30
Clearly 3m = 3 × 5 = 15{is not matching Σf(i)} But
3n = 3 × 10 = 30 {is matching Σf(i) = 30}
∴ 3 n is the only correct answer.
The correct choice is (b).
The problem can also be solved in a more general way as follows:
\(\sum_{i=1}^{m} f(i)\) = f(1) + f(2) + ……+ f(m)
Since, f(1) = f(2) =…….= f(m) = (m-1)C2
= \(\frac{\mathrm{m} \times(\mathrm{m}-1) \times(\mathrm{m}-2)}{2}\)
= \(\frac{3 \times \mathrm{m} \times(\mathrm{m}-1) \times(\mathrm{m}-2)}{1 \times 2 \times 3}\)
= 3 × mC3
Since n = Number of there elements subsets of a set of m elements = mC3
Therefore, \(\sum_{i=1}^{m} f(i)\) = 3 × mC3 = 3n
Question 56.
Let P, Q, and R be set to let △ denote the symmetric difference operator defined as P △ Q = (P ∪ Q) — (P ∩ Q). Using Venn diagrams, determine which of the following is/are TRUE?
I. P △ (Q ∩ R) = (P △ Q) ∩ (P △ R)
II. P ∩ (Q △ R) = (P ∩ Q) △ (P ∩ R)
(a) I only
(b) II only
(c) Neither I nor II
(d) Both I and II
Answer/Explanation
Answer: (b) II only
Explanation:
P △ Q = PQ’ + P’Q
where △ is symmetric difference between P and Q.
I. LHS = P △ Q ∩ R = P△(QR) = P(QR)’ + P'(QR) = P(Q’ + R’) + P’QR
RHS = (P △ Q) ∩ (P △ R) = (PQ’ + P’Q) (PR’ + P’R) = PQ’R’ + P’QR
LHS ≠ RHS So statement I is false.
II. LHS = P ∩ Q △ R = P(QR’ + Q’R)
= PQR’ + PQ’R
RHS = (P ∩ Q) △ (P ∩ R) = PQ △ PR = PQ(PR)’ + (PQ)’ PR = PQ(P’ + R’) + (P’+Q’)PR = PQR’ + PQ’R
LHS = RHS
So statement II is true.
Question 57.
What is the cardinality of the set of integers X defined below? X = {n| 1 ≤ n ≤ 123, n is not divisible by 2, 3 or 5}
(a) 28
(b) 33
(c) 37
(d) 44
Answer/Explanation
Answer: (b) 33
Explanation:
We know that, number of elements divisible by number ‘x’ in set of integer (from 1 to X) = \(\frac{X}{x}\)
So, according to inclusion exclusion formula:
n(2 or 3 or 5) = n(2) + n(3) + n(5) – n(2,3) – n(2,5) – n(3,5) – n (2,3,5))
No’s divisible by 2 in X = \(\left[\frac{123}{2}\right\rfloor\) = 61
No’s divisible by 3 in X = \(\left[\frac{123}{3}\right\rfloor\) = 41
No’s divisible by 5 in X = \(\left[\frac{123}{5}\right\rfloor\) = 24
No’s divisible by 2 and 3 = \(\left.\mid \frac{123}{2 \times 3}\right\rfloor\) = \(\left[\frac{123}{6}\right\rfloor\) = 20
No’s divisible by 3 and 5 = \(\left.\mid \frac{123}{3 \times 5}\right\rfloor\) = \(\left[\frac{123}{15}\right\rfloor\) = 8
No’s divisible by 2 and 5 = \(\)
No’s divisible by 2 and 3 and 5
The problem can be solved by considering the cases m = 4 and m = 5 etc.
= \(\left[\frac{123}{2 \times 3 \times 5}\right\rfloor\) = \(\left[\frac{123}{30}\right\rfloor\) = 4
So, n(2 or 3 or 5) = 61 + 41 +24 — 20 — 8-12 + 4 = 90
n(2 or 3 or 5) = Total number – n(2 or 3 or 5) = 123-90 = 33
![]()
Question 58.
Let S be a set of n elements. The number of ordered pairs in the largest and the smallest equivalence relations on S is
(a) n and n
(b) n2 and n
(c) n2 and 0
(d) n and 1
Answer/Explanation
Answer: (b) n2 and n
Explanation:
Let S be a set of n elements say {1, 2, 3,…, n}. Now the smallest equivalence relation on S must contain all the reflexive elements {(1, 1), (2, 2), (3, 3),…, (n, n)} and its cardinality is therefore n. The largest equivalence relation on S is S × S, which has a cardinality of n × n = n2.
∴ The largest and smallest equivalence relations on S have cardinalities of n2 and n respectively. The correct choice is (b).
Question 59.
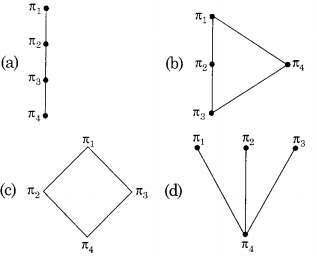
Consider the set S = {a, b, c, d}. Consider the following 4 partitions π1 ,π2, π3, π4 on
S: π1 = \(\{\overline{a b c d}\}\) , π2 = \(\{\overline{a b}, \overline{c d}\}\) , π3 = \(\{\overline{a b c}, \bar{d}\}\) , π4 = \(\{\bar{a}, \bar{b}, \bar{c}, \bar{d}\}\)
Let ≺ be the partial order on the set of partitions S’ = (π1 ,π2, π3, π4) defined as follows: πi≺ πj if and only if πi refines πj The poset diagram for (S’, ≺) is
Answer/Explanation
Answer: (c)
Explanation:
A partition P1 is called a refinement of the partition P2 if every set in P1, is a subset of one of the sets in P2.
π4 is a refinement of π2,π3, and π1
π2 and n3 are refinements of π1
π2 and π3 are not comparable since neither is a refinement of the other.
So the poset diagram for (S’, <) would
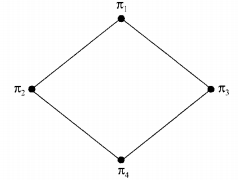
Which is choice (c).
Question 60.
A partial order P is defined on the set of natural numbers as follows. Here x/y denotes integer division.
(i) (0, 0) ∈P.
(ii) (a, b) ∈P if and only if a %10 ≤ b %10 and (a/10, b/10) ∈P.
Consider the following ordered pairs:
(i) (101, 22)
(ii) (22, 101)
(iii) (145, 265)
(iv)(0, 153)
Which of these ordered pairs of natural numbers are contained in P?
(a) (i) and (iii)
(b) (ii) and (iv)
(c) (i) and (iv)
(d) (iii) and (iv)
Answer/Explanation
Answer: (d) (iii) and (iv)
Explanation:
In this problem
a % b means the mod function (i.e. residue when a is divided by b).
a/b means integer division (i.e. quotient when a is divided by b)
(i) (101,22):
101% 10 ≤ 22% 10 ⇒ 1 ≤ 2 which is true. (101/10, 22/10) = (10, 2) ∈ P need to check IS (10, 2) ∈ P?
10% 10 ≤ 2% 10 ⇒ 0 ≤ 2 which is True.
Then (10/10, 2/10) = (1, 0) fails since 1 < 0.
∴ (101, 22) ∉ P.
(ii) (22, 101)
22% 10 ≤ 101% 10 ⇒ 2 ≤ 1 is False.
∴ (22, 101)∉ P
(iii) (145, 265)
145% 10 ≤ 265% 10 ⇒ 5 ≤ 5 is true and (145/10, 265/10) = (14, 26) e P has to be checked.
Now consider (14, 26).
14% 10 ≤ 26% 10 ⇒ 4 ≤ 6 is true and (14/10, 26/10) = (1, 2) ∈ P has to be checked. Now consider (1, 2)
1% 10 ≤ 2% 10 ⇒ 1 ≤ 2 is true and (1/10, 2/10) = (0, 0) ∈ P which is given to be true. Therefore (145, 265) ∈ P.
(iv) (0, 153):
0% 10 ≤ 153% 10 ⇒ 0 ≤ 3 is true.
Then (0/10, 153/10) = (0, 15) should be in P. (0, 15):
0% 10 ≤ 15% 10 ⇒ 0 ≤ 5 is true.
Then (0/10, 15/10) = (0, 1) should be in P. (0, 1):
0% 10 ≤ 1% 10 ⇒ 0 ≤ 1 is true.
Then (0/10, 1/10) = (0, 0) should be in P. It is given that (0, 0) ∈ P Therefore (0, 153) ∈ P.
So (iii) and (iv) are contained in P.
Question 61.
If P, Q, R are subsets of the universal set
U, then (P∩Q∩R) ∪ (Pc ∩ Q ∩ R) ∪ Qc ∪ Rc is
(a) Qc ∪ Rc
(b) P ∪ Qc ∪ Rc
(c) Pc ∪ Qc ∪ Rc
(d) U
Answer/Explanation
Answer: (d) U
Explanation:
The given set theory expression can be converted into equivalent boolean algebra expression as follows:
(p∩q∩r) ∪ (pc ∩ q ∩ r) ∪ qc ∪ rc
= p.q.r + p’.q.r + q’ + r’
= qr (p + p’) + q’ + r’
= qr + q’ + r’
= (q + q’) . (r + q’) + r’
= r + q’ + r’
= r + r’ + q’
= 1 + q’
= 1 = U
![]()
Question 62.
Consider the following Hasse diagrams.
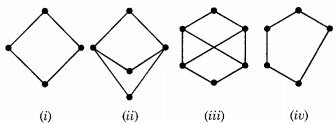
Which all of the above represent a lattice?
(a) (i) and (iv) only
(b) (ii) and (iii) only
(c) (iii) only
(d) (i), (ii) and (iv) only
Answer/Explanation
Answer: (a) (i) and (iv) only
Explanation:
In lattice, every pair in the Hasse diagram must have Least Upper Bound (LUB) and Greatest Lower Bound (GLB). In figure
For element d, e LUB (d, e) = {b, c} but LUB must be unique i.e. only 1 element present in LUB. Same for GLB (b, c) = {d, e} Hence not lattice.
GLB (b, d) = {c, e} but GLB must be unique i.e. only 1 element present in GLB. Hence not lattice. So, (ii) and (iii) are not lattice
Question 63.
Which one of the following is NOT necessarily a property of a Group?
(a) Commutativity
(b) Associativity
(c) Existence of inverse for every element
(d) Existence of identity
Answer/Explanation
Answer: (a) Commutativity
Explanation:
Group properties are closure, associativity existence of identity, and existence of inverse for every element. Commutativity is not required for a mathematical structure to become a group.
Question 64.
Consider the binary relation: R = {(x, y), (x, z), (z, x), (z, y)} on the set {x, y, z}. Which one of the following is TRUE?
(a) R is symmetric but NOT antisymmetric
(b) R is NOT symmetric but antisymmetric
(c) R is both symmetric and antisymmetric
(d) R is neither symmetric nor antisymmetric
Answer/Explanation
Answer: (d) R is neither symmetric nor antisymmetric
Explanation:
Given, R {(x, y), (x, z), (z, x), (z, y)) on set {x, y, z}, here (x, y) ∈ R and (y, x) ∉ R.
∴ R is not symmetric
Also(x, z)ER and(z, x) ∈ R.
∴ R is not an autism metric.
R is neither symmetric nor anti-symmetric.
Question 65.
The composition table of a cyclic group is shown below:
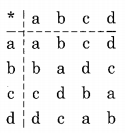
Which one of the following choices is correct?
(a) a, b are generators
(b) b, c are generators
(c) c, d are generators
(d) d, a are generators
Answer/Explanation
Answer: (c) c, d are generators
Explanation:
If an element is a generator, all elements must be obtained as powers of that element.
Try a, b, c, d one by one to see which are the generators.
a = a
a2 = a.a = a
a3 = a.a2 = a.a = a and so on.
∴ a is not the generator,
b = b
b2 = b.b = a
b3 = b.b2 = b.a = b
b4 = b.b3 = b.b = a and so on
∴ b is not the generator c = c
c2 c.c = b
c3 = c.c2 = c.b = d
c4 = c.c3 = c.d = a
Since all of a, b, c, d have been generated as powers of c
∴ c is a generator of this group.
Similarly,
d = d
d2 = d.d = b
d3 = d.d2 d.b = c
d4 = d.d3 = d.c a
∴ d is the other generator.
![]()
Question 66.
What is the possible number of reflexive relations on a set of 5 elements?
(a) 210
(b) 215
(c) 220
(d) 225
Answer/Explanation
Answer: (c) 220
Explanation:
A number of reflexive relations on a set with n elements = 2n² – n.
Here n = 5. So, answer is 25² – 5 = 220.
Question 67.
Consider the set S = {1, ω, ω2}, where ω and ω2 are cube roots of unity. If * denotes the multiplication operation, the structure {S, *} forms
(a) a group
(b) a ring
(c) an integral domain
(d) a field
Answer/Explanation
Answer: (a) a group
Explanation:
The structure ({n, nth roots of unity}, ×) always forms a group. When n = 3 we get the set ({1, w, w2}, ×) which must also form a group.
or
The fact that ({1, w, w2}, × ) forms a group can also be seen by the fact that it satisfies the four group properties.
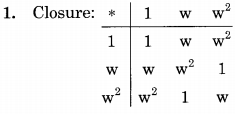
From the above operation table, we can see that the given operation is closed, on the given set.
2. Associative: “*” is an associative operation.
3. Identity: From the operation table, we can see that the identity element, is “1”.
4. Inverse: From the operation table, we can see that the inverse of 1 is 1, the inverse of w is w2 and the inverse of w2 is w.
So, ({1, w, w2}, *) is a group.
To be a ring, integral domain, or field, we need two binary operations to be specified, whereas here we have only one operation given. So, choice (a) is correct.
Question 68.
How many onto (or surjective) functions are there from an n-element (n ≥ 2) set to a 2-element set?
(a) 2n
(b) 2n – 1
(c) 2n– 2
(d) 2(2n-2)
Answer/Explanation
Answer: (c) 2n– 2
Explanation:
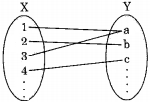
Let n = 2. There are only 2 onto functions as shown below:
For, n = 2
Option (a) 2n = 22 = 4
Option (b) 2n – 1 = 22 – 1 = 3
Option (c) 2n — 2 = 22 — 2 = 2
Option (d) 2(2n — 2) = 2(22 – 2) = 4
So only option (c) gives correct answer.
Alternate method:
The number of onto functions from a set A with m elements to set B with n elements where n < m is given by
nm – nC1(n- 1)m+ nC2(n —2)m … + nCn- 1 1m
Here, m = n = 2
So number of onto functions = 2n—2C1 1m = 2n – 2
which is choice (c).
Question 69.
A binary operation ⊕ on a set of integers is defined as x ⊕ y = x2 + y2. Which one of the following statements is TRUE about ⊕?
(a) Commutative but not associative
(b) Both commutative and associative
(c) Associative but not commutative
(d) Neither commutative nor associative
Answer/Explanation
Answer: (a) Commutative but not associative
Explanation:
x ⊕ y = x2 + y2
y ⊕ x = y2 + x2
As ‘+’ sign in commutative so x2 + y2 is equal to y2 + x2 so x ⊕ y is commutative.
Now check associativity
x ⊕ (y ⊕ z) = x ⊕ (y2 + z2)
= x2 + (y2 + z2)2
= x2 + y4 + z4 + 2y2z2
(x ⊕ y) ⊕ z = (x2 + y2) ⊕ z
= (x2 + y2)2 + z2
= x4 + y4 + 2x2y2 + z2
x ⊕ (y ⊕ z) t- (x ⊕ y) ⊕ z
So not associative Option (a) is correct.
![]()
Question 70.
Let S denote the set of all functions f: {0, 1}4 → {0,1}. Denote by N the number of functions from S to the set {0, 1}. The value of log2 log2N is ______.
Answer/Explanation
Explanation:
f : {0, 1}4 → {0,1} ⇒ S is the set of all functions from a 16 element set to a 2 element set.
| S | =216
N = Number of functions from S to 2 element set {0, 1} = 2216 ]
N = 22
∴ log log N = log log 22’6 = log2216 = 16
Question 71.
Consider the following relation on subsets of the set S of integers between 1 and 2014. For two distinct subsets U and U of S we say U Consider the following two statements:
S1: There is a subset of S that is larger than every other subset.
S2: There is a subset of S that is smaller than every other subset.
Which one of the following is CORRECT?
(a) Both S1 and S2 are true
(b) S1 is true and S2 is false
(c) S2 is true and S1 is false
(d) Neither S1 nor S2 is true
Answer/Explanation
Answer: (a) Both S1 and S2 are true
Explanation:
Given the following details:
S = {1,2,3,4,. ..2014}
U < V if the minimum element in the symmetric difference of the two sets is in U.
S1: There is a subset of S that is larger than every other subset.
S2: There is a subset of S that is smaller than every other subset.
S1 is true since Φ (which is a subset of S) is larger than every other subset.
i.e. ∀u v < Φ is true since the minimum element in v △ Φ = v, is in v.
(Note: v △ Φ = uΦ + v’Φ = v)
S2 is also true since S (which is a subset of S) is smaller than every other subset, i.e. ∀u S < v is true since the minimum element in S △ v = v’, is in <S.
(Note: S △ v = Sv’ + S’v = lv’ + Ov =v’)
∴ Both S1 and S2 are correct.
Question 72.
Let X and Y be finite sets and f: X → Y is a function. Which one of the following statements is TRUE?
(a) For any subsets A and B of X, | f(A ∪ B)| = |f(A)| + |f(B)|
(b) For any subsets A and B of X, |f(A ∪ B) = |f(A)| + |f(B)|
(c) For any subsets A and B of X, |f(A ∩ B)| = min{|f(A)|,|f(B)|}
(d) For any subsets S and Tof Y, f-1(S ∩ T) = f -1(S) ∩ f-1(T)
Answer/Explanation
Answer: (d) For any subsets S and Tof Y, f-1(S ∩ T) = f -1(S) ∩ f-1(T)
Explanation:
Example:
Let A = {1, 2}, B = {3, 4}
(a) |f (A ∪ B)| = |f(A) |+ |f(B)|
⇒ 3 = 2 + 2 is false
(b) f (A ∩ B) = f (A) ∩ f (B)
⇒ Φ = {a} is false
(c) |f(A ∩ B)| =min{|f(A)|, |f(B)|}
⇒ 0 = min (2, 2) = 2 is false
(d) Let S = {a, b}, T- {a, c}
f-1 (S ∩ T)=f-1(S)∩ f-1(T)
⇒ {1, 3} = {1, 2, 3} n {1, 3, 4}
⇒ {1, 3} = {1, 3} is true
Question 73.
Let G be a group with 15 elements. Let L be a subgroup of G. It is known that L ≠ G and that the size of L is at least 4. The size of L is _____.
Answer/Explanation
Explanation:
Order of subgroup divides the order of group (Lagrange’s theorem). So the order of L has to be 1, 3, 5, or 15. As it is given that the subgroup has at least 4 elements and it is not equal to the given group, therefore the order of the subgroup can’t be 1, 3, or 15. Hence it is 5.
Question 74.
Consider the set of all functions f : {0,1, …, 2014} → {0,1, …,2014} such that f(f(i)) = i, for all 0≤i≤ 2014. Consider the following statements:
P: For each such function it must be the case that for every i, f(i) = i.
Q: For each such function it must be the case that for some i, f(i) = i.
R: Each such function must be onto.
Which one of the following is CORRECT?
(a) P, Q, and R are true
(b) Only Q and R are true
(c) Only P and Q are true
(d) Only R is true
Answer/Explanation
Answer: (b) Only Q and R are true
Explanation:
Since it is given that ∀i f(f(i)) = i
It means f . f = I i.e. f = f’-1 That is f is a symmetric function.
Statement P means that every symmetric function is an identity function which is false since there are many symmetric functions other than the identity function.
Example: {(0,1), (1,0), (2, 3), (3,2),…(2012,2013),(2013, 2012), (2014, 2014)} is a symmetric function but not the identity function.
Statement Q means that in every such symmetric function at least one element is mapped to itself and this is true since there is an odd number of elements in the set {0, 1, 2, … 2014}.
Statement R means that every symmetric function is onto which is true since it is impossible to make an into function symmetric. See the below diagram for an into function shown with only 3 elements:
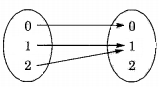
In the above function note that (2, 1) exists in the function but not (1,2) and so it is not symmetric.
Question 75.
There are two elements x,y in a group (G, *) such that every element in the group can be written as a product of some number of x’s and y’s in some order. It is known that x*x = y*y = x*y*x*y = y*x*y*x = e where e is the identity element. The maximum number of elements in such a group is______.
Answer/Explanation
Explanation:
(i) e is identity element
(ii) x*x = e, so x = x-1.
(iii) y*y = e, so y = y-1.
(iv) (x*y)*(x*y) = e, so x*y = (x*y)-1 and (y*x)*(y*x) = e, so y*x = (y*x)-1.
Now (x*y)*(y*x) = x*(y*y)*x = x*e*x = x*x = e
So, (x*y)-1. = (y*x)
From (i) and (ii) we get x*y* = y*x
There are only 4 distinct elements possible in this group
1. e
2. x
3. y
4. xy
All other combinations are equal to one of these four as can be seen below:
yx = xy (already proved)
xxx = xe = x
xyy = xe = x
xxy = ey = y
xyx = xxy = y
and so on…….
So the group is G = {e, x, y, x*y
⇒ |G| = 4
![]()
Question 76.
If g(x) =1 -x and h(x) = \(\frac{x}{x-1}\) , then \(\frac{g(h(x))}{h(g(x))}\) is
(a) \(\frac{h(x)}{g(x)}\)
(b) \(\frac{-1}{x}\)
(c)\(\frac{g(x)}{h(x)}\)
(d) \(\frac{x}{(1-x)^{2}}\)
Answer/Explanation
Answer: (a) \(\frac{h(x)}{g(x)}\)
Explanation:
g(x) = 1 – x, h(x) = \(\frac{x}{x-1}\)
\(\frac{g(h(x))}{h(g(x))}\) = \(\frac{g\left(\frac{x}{x-1}\right)}{h(1-x)}\) = \(\frac{1-\frac{x}{x-1}}{\frac{1-x}{1-x-1}}\) = \(\frac{x-1-x}{\frac{x-1}{\frac{1-x}{-x}}}\) = \(\frac{\frac{-1}{x-1}}{\frac{1-x}{-x}}\) = \(\frac{x}{(x-1)(1-x)}\) = \(\frac{-x}{(1-x)^{2}}\)
\(\frac{h(x)}{g(x)}\) = \(\frac{x}{\frac{x-1}{1-x}}\) = \(\frac{x}{(1-x)(x-1)}\) = \(\frac{-x}{(1-x)^{2}}\)
∴ \(\frac{g(h(x))}{h(g(x))}\) = \(\frac{h(x)}{g(x)}\)
Question 77.
For a set A, the power set of A is denoted by 2A. If A = {5, {6}, {7}}, which of the following options are True?
1. Ø ∈ 2A
2. Ø ⊆ 2A
3. {5,{6}} ∈ 2A
4. {5,{6}} ⊆ 2A
(a) 1 and 3 only
(b) 2 and 3 only
(c) 1, 2 and 3 only
(d) 1, 2 and 4 only
Answer/Explanation
Answer: (c) 1, 2, and 3 only
Explanation:
A = {5, {6}, {7}}
1. Φ ∈ 2A is true. Any power set contains an empty set.
2. Φ ⊆ 2A is true. Empty set is subset of any set.
3. {5, {6}}e 2A is true, power set of A contain {5, {6}} as a 2 element subset of A.
4. {5, {6}} ⊆ 2A is false. Power set of A not contain 5 and {6} as elements.
So {5, {6}} can not be subset of 2A.
Question 78.
Suppose L = {p,q, r, s, t} is a lattice represented by the following Hasse diagram:
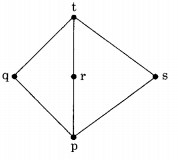
For any xy ∈ L, not necessarily distinct, x ∨ y and x ∧ y are join and meet of x, y respectively. Let L<sup>3</sup> = {(x,y,z): x, y, z ∈ L} be the set of all ordered triplets of the elements of L. Let pr be the probability that an element (x,y,z) e L<sup>3</sup> chosen equiprobably satisfies x ∨ (y ∧ Z) = (x ∨ y) ∧ (x ∨ z). Then
(a) P<sub>r</sub> = 0
(b) p<sub>r</sub> = 1
(c) 0<p<sub>r</sub>≤\(\frac { 1 }{ 5 }\)
(d) \(\frac { 1 }{ 5 }\) < p<sub>r</sub> < 1
Answer/Explanation
Answer: (d) \(\frac { 1 }{ 5 }\) < p<sub>r</sub> < 1
Explanation:
L has 5 elements
L3 has all ordered triplets of elements of L
⇒ L3 contain 5 × 5 × 5 = 53 = 125 elements.
If q, r, s are chosen, then only it will violate the distributive property. Number of ways to choose q, r, s in any triplet order = 3! = 3 × 2 × 1 = 6.
∴ p(satisfying distributive property)
= 1 – p(violate the distributive property)
= 1 – \(\frac{6}{5^{3}}\) = 0.952 which is between \(\frac{1}{5}\) and 1.
Question 79.
Let R be the relation on the set of positive integers such that aRb if and only if a and b are distinct and have a common divisor other than 1. Which one of the following statements about R is True?
(a) R is symmetric and reflexive but not transitive
(b) R is reflexive but not symmetric and not transitive
(c) R is transitive but not reflexive and not symmetric
(d) R is symmetric but not reflexive and not transitive
Answer/Explanation
Answer: (d) R is symmetric but not reflexive and not transitive
Explanation:
aRb iff a and b are distinct a and b have a common divisor other than 1.
(i) R is not reflexive since a and b are distinct i.e, (a, a) ∉ R
(ii) R is symmetric If a and b are distinct and have a common divisor other than 1, then b and a also are distinct and have a common divisor other than 1.
(iii) R is not transitive
If (a, b) ∈ R and (b, c) ∈ R then (a, c) need not be in R.
Example: (2, 6) ∈ R and (6, 2) ∈ R, but (2, 2) ∉ R
∴ R is symmetric but not reflexive and not transitive.
Question 80.
The cardinality of the power set of {0, 1,2…, 10} is _____.
Answer/Explanation
Explanation:
Let X = {0, 1,2,…..10}
|X| = 1
|P(X)| = 211 = 2048
![]()
Question 81.
The number of onto functions (surjective functions) from set X = {1,2,3,4} to set Y = {a, b, c} is _____.
Answer/Explanation
Explanation:
The number of onto functions from A → B where | A | = m and | B | = n is given by the formula
nm – nC1(n – 1)m + nC2(n – 2)m +…
+ (-1)n – 1 nCn – 11m
Here, m = 4 and n = 3
Substituting in above formula we get, 34 – 3C1(3 – 1)4 + 3C2 (3 – 2)4 = 81 – 48 + 3 = 36
Question 82.
Let X and Y denote the sets containing 2 and 20 distinct objects respectively and F denote the set of all possible functions defined from X and Y. Let f be randomly chosen from F. The probability of f being one-to-one is _______.
Answer/Explanation
Explanation:
Total possible functions = 202 = 400
Number of one-to-one functions = 20P2 = 20 × 19
∴ Required probability = \(\frac{20 \times 19}{20 \times 20}\) = 0.95
Question 83.
Let # be a binary operator defined as X # Y = X’ + Y’ where X and Y are Boolean variables. Consider the following two statements:
S1:(P # Q) # R = P # (Q # R)
S2:Q # R = R # Q
Which of the following is/are true for the Boolean variables P, Q, and R?
(a) Only S1 is True
(b) Only S2 is True
(c) Both S1 and S2 are True
(d) Neither S1 nor S2 is True
Answer/Explanation
Answer: (b) Only S2 is True
Explanation:
X # Y = X’ + Y’
This is the NAND operation. NAND is known to be commutative but not associative. So, only S2 is true.
Question 84.
Suppose U is the power set of the set S = {1,2,3,4,5,6}. For any Te U, let | T| denote the number of elements in T and T’ denote the complement of T. For any T, R ∈ U, let T \ R be the set of all elements in T which are not in R. Which one of the following is true?
(a) ∀X ∈ U(|X| = |X’|)
(b) ∃X ∈ U ∃Y ∈U(|X|= 5, |Y|=5 and X ∩ Y = 0)
(c) ∀X ∈ U ∀Y ∈U(|X |=2,| Y|=3 and Y\F = 0)
(d) ∀X ∈U ∀ Y ∈U(X\Y =Y’\X’)
Answer/Explanation
Answer: (d) ∀X ∈U ∀ Y ∈U(X\Y =Y’\X’)
Explanation:
S = {1, 2, 3, 4, 5, 6}
U is the power set of S ⇒ U = P(S)
U ={{ } {1}, {2}, …{1, 2}, {1, 3}, …{1, 2, 3}, … {1, 2, 3, 4}, …{1, 2, 3, 4, 5} …{1, 2, 3, 4, 5, 6}}
| U |= 26 = 64 elements.
T ∈ U ⇒ T’ ∈ U
R ∈U, T\R=T – R
(a)∀X ∈ U(| X | = | X’ |) means that every subset of S has same size as its complement. Clearly this is False.
(For example, {1} ∈ U, and complement of {1} = {2, 3, 4, 5, 6})
(b)∃X ∈ U∃Y ∈ U(|X|=5,|Y|=5 and X ∩ Y = Φ) means that there are two 5 element subsets of S which have nothing in common. This is clearly False.
Since any two 5 element subsets will have atleast 4 elements in common.
(c) ∀X ∈ U ∀ Y ∈ U(|X| = 2,|y|=3 and X\Y = Φ) means that every 2 element subset X and every 3 element subset Y will have X – Y = Φ i.e., X ⊆ Y.
This is clearly False as can be seen from the example X= {1,2}, Y = {3,4,5} where X’^Y.
(d) ∀X ∈ U ∀T ∈ U(X \Y = Y’\X’) means that for any two subsets X and Y, X\ Y = Y \ X’ i.e. X – Y = Y’ – X’.
This is clearly True since by boolean algebra LHS = X – Y = XY’.
RHS =Y’ -X’ = Y’Xand therefore LHS = RHS.
![]()
Question 85.
Let R be a relation on the set of ordered pairs of positive integers such that ((p, q), (r, s)) ∈ R if and only if p – s = q — r. Which one of the following is true about R?
(a) Both reflexive and symmetric
(b) Reflexive but not symmetric
(c) Not reflexive but symmetric
(d) Neither reflexive nor symmetric
Answer/Explanation
Answer: (c) Not reflexive but symmetric
Explanation:
R = {(p, q), (r, s) I p – s = q – r}
(i) Check reflexive property
∀(p, q) ∈ Z+ × Z+ ((p, q), (p, q)) ∈ R
is true iff p – q = q – p which is false. So relation R is not reflexive.
(ii) Check symmetry property
If ((p, q), (r, .s’))∈ R then ((r, s), (p, q)) ∈ R
((p, q), (r, s)) ∈ R ⇒ p – s = q – r
((r, s), (p, q)) ∈ R ⇒ r – q = s – p
If p – s = q – r is true, then r — q = s – p is also true by rearranging the equation.
∴ R is symmetric.
Question 86.
A function f : N++ → N+, defined on the set of positive integers N+, satisfies the following properties:
f(n) – f(nl2) if n is even
f(n) = f(n + 5) if n is odd
Let R = {i | ∃ j : f (j) = i} be the set of distinct values that/takes. The maximum possible size of R is _______.
Answer/Explanation
Explanation:
f(n) = f\(\left(\frac{n}{2}\right)\) if n is even
f(n) = f{n + 5) if n is odd
f : N+ → N+
Now f(2) = f\(\left(\frac{2}{2}\right)\) = f(1)
f(3) = f(3 + 5) = f(8) = f\(\left(\frac{8}{2}\right)\) = f(4) = f\(\left(\frac{4}{2}\right)\) = f(2) = (1)
So, f(1) = f(2) = f(3) = f(4) = f(8)
Now let us find f(5) = f(5 +5) = f(10) = f\(\left(\frac{10}{2}\right)\)
= f(5) so f(5) = f(10)
Now let us find f(9)
f(9) = f(9 +5) = f(14) = f\(\left(\frac{14}{2}\right)\) = f(7)
= f(7 + 5) = f(12) = f\(\left(\frac{12}{2}\right)\) = f(6)
= f\(\left(\frac{6}{2}\right)\) = f(3)
So f(9) = f(7) = f(6) = f(3) = f(1) = f(2) = f(4) = f(8)
For n > 10, the function will be equal to one of f(1), f(2)….f(10)
So the maximum no. of distinct values / takes is only 2.
First is f(1) = f(2) = f(3) = f(4) = f(8) = f(9) = f(7) = f(6)
Second is f(5) = f(10)
All other n values will give only one of these two values.
Question 87.
A binary relation R on N × N is defined as follows: (a, b) R (c, d) if a ≤ c or b ≤ d. Consider the following propositions:
P: R is reflexive
Q: R is transitive
Which one of the following statements is TRUE?
(a) Both P and Q are true
(b) P is true and Q are false
(c) P is false and Q are true
(d) Both P and Q are false
Answer/Explanation
Answer: (b) P is true and Q are false
Explanation:
(a, b) R (c, d) if a ≤ c or b ≤ d
P : R is reflexive
Q : R is transitive
Since, (a, b) R (a, b) ⇒ a ≤ a or b ≤ b ⇒ t or t
Which is always True, R is reflexive. Now let us check transitive property
Let(a,b) R (c, d) ⇒ a ≤ c or b ≤ d
and(c, d) R {e, f) ⇒ c ≤ e or d ≤ f
Now let us take a situation
a ≤ c (True) or b ≤ d ( false)
and c ≤ e (False) or d ≤ f (True)
Now we can get neither a ≤ e nor b ≤ f So, (a, b) R (c, d) and (c, d) R (e, f) ≠ (a, b) R (e, f). So clearly R is not transitive.
So Pis true and Q is false. Choice (b) is correct.
Question 88.
Consider a set U of 23 different compounds in a Chemistry lab. There is a subset S of U of 9 compounds, each of which reacts with exactly 3 compounds of U. Consider the following statements:
I. Each compound in U \ S reacts with an odd number of compounds.
II. At least one compound in U \S reacts with an odd number of compounds.
Ell. Each compound in U\S reacts with an even number of compounds
Which one of the above statements is ALWAYS TRUE?
(a) Only I
(b) Only II
(c) Only III
(d) None of these
Answer/Explanation
Answer: (b) Only II
Explanation:
This is actually a graph theory Question. Let the components be represented by vertices and if component x reacts with component y then let there be an undirected edge between x and y.Now, 9 of the 23 vertices will have 3 degrees each.
Note: U \ S means U — S, which is the remaining 23 – 9 = 14 vertices.
By Handshaking theorem,
9 × 3 + degree of 14 vertices = 2e = Even. i.e., 27 + degree of 14 vertices = 2e = Even. So, the total degree of 14 vertices must be odd.
Statement I means that the degree of each of the 14 vertices is odd, which means that the total degree of 14 vertices will be even (since even number of odd numbers is always even). But we need the total degree of 14 vertices to be odd so, statement I is false.
Statement III means that everyone of the 14 vertices has even degree, which guarantees that the total degree of 14 vertices will be even. So, statement III is false. Since statement II is the negation of statement III, it must be true.
Question 89.
Consider the set X = {a, b, c, d, ej under the partial ordering:
R = {(a, a), (a, b), (a, c), (a, d), (a, e), (b, b), (b, c), (b, e), (c, c), (c, e), (d, d), (d, e), (e, e)}.
The Hasse diagram of the partial order (X, R) is shown below:
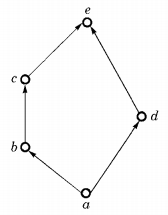
The minimum number of ordered pairs that need to be added to R to make (X, R) a lattice is ______.
Answer/Explanation
Explanation:
Since the given hasse diagram is already a lattice, three is no need to add any ordered pair. So the answer is 0.
![]()
Question 90.
The number of integers between 1 and 500 (both inclusive) that are divisible by 3 or 5 or 7 is ______.
Answer/Explanation
Explanation:
Let A → -5- by 3
B → ÷ by 5
C →÷ by 7
n(A ∪ B ∪ C) = n(A)+n(B) + n(C) – n(A ∩ B) – n(A ∩ C) – n(B ∩ C) + n(A ∩ B ∩ C)
= \(\left[\frac{500}{3}\right\rfloor\) + \(\left[\frac{500}{5}\right\rfloor\) + \(\left[\frac{500}{7}\right\rfloor\) – \(\left[\frac{500}{15}\right\rfloor\) – \(\left[\frac{500}{21}\right\rfloor\) – \(\left[\frac{500}{35}\right\rfloor\) + \(\left[\frac{500}{105}\right\rfloor\) = 166 + 100 + 71 – 33 – 23 – 14 + 4 = 271
Question 91.
Let G be a finite group on 84 elements. The size of the largest possible proper subgroup of G is _______.
Answer/Explanation
Explanation:
Given | G | =84
By Lagrang’s theorem any subgroup size is a divisior of 84.
But a proper subgroup cannot have same size as group.
So largest divisor of 84, other than 84 is 42. So, largest proper subgroup can have in size of 42.
Question 92.
Let N be the set of natural numbers. Consider the following sets:
P. Set of Rational numbers (positive and negative).
Q. Set of functions from {0, 1} to N.
R. Set of functions from N to {0, 1}.
S. Set of finite subsets of N.
Which of the sets above is countable?
(a) Q and S only
(b) P and S only
(c) P and R only
(d) P, Q, and S only
Answer/Explanation
Answer: (d) P, Q, and S only
Explanation:
P: Set of rational number → countable
Q: Set of functions from {0, 1} to N → N
0 can be assigned in N ways
1 can be assigned in N ways
There are N × N functions, the cross product of countable set in countable.
R: Set of functions from N to {0,1}

Each of these boxes can be assigned to 0 or 1 so each such function is a binary number with an infinite number of bits.
Example: 0000 is the binary number corresponding to 0 is assigned to all boxes and so on. Since each such binary number represents a subset of N (the set of natural numbers) by characteristic function method, therefore, the set of such function is the same as the power set of N which is uncountable due to Cantor’s theorem, which says that power set of a countably infinite set is always uncountably infinite.
S: Set of finite subsets of N → countably infinite since we are counting only finite subsets. So P, Q, and S are countable.
Question 93.
Let G be an arbitrary group. Consider the following relations on G:
R1: ∀a, b ∈ G, a R1 b if and only if ∃g ∈ G such that a = g-1 bg
R2: ∀a, b ∈ G, a R2 b if and only if a = b-1
Which of the above is/are equivalence relation/ relations?
(a) R1 and R2
(b) R1 only
(c) R2 only
(d) Neither R1 nor R2
Answer/Explanation
Answer: (b) R1 only
Explanation:
R1: ∀a, b ∈ G,a R1 b if and only if ∃g∈ G such that a = g-1bg
Reflexive: a = g-1ag can be satisfied by putting g = e, identity “e” always exists in a group.
So reflexive
Symmetric: aRb ⇒ a = g-1ag for some g
⇒ b = gag-1 = (g-1)-1 ag-1 g-1 always exists for every g ∈ G.
So symmetric
Transitive: aRb and bRc ⇒ a = g1-1bg1 and b = g2-1 cg2 for some g1g2 ∈ G.
Now a=g1-1g2-1cg2g1(g2g1)-1 cg2g1
g1 ∈ G and g2 ∈ G ⇒ g2g1 ∈ G since group is closed so aRb and aRb ⇒ aRc hence transitive
Clearly R1 is equivalence relation.
R2 is not equivalenced it need not even be reflexive, since aR2 a => a = a-1 ∀a which not be true in a group.
R1 is equivalence relation is the correct answer.
Question 94.
Let R be the set of all binary relations on the set {1, 2, 3}. Suppose a relation is chosen from R at random. The probability that the chosen relation is reflexive (round off to 3 decimal places) is _____.
Answer/Explanation
Explanation:
A = {1, 2, 3}
n = |A| = 3
Number of relations on A = 2n² = 23² = 29
Number of reflexive relations on A
= 2n² – n = 23² – 3 = 26
Question 95.
Let G be a group of 35 elements. Then the largest possible size of a subgroup of G other than G itself is _______.
Answer/Explanation
Explanation:
Size of group = O(G) = 35
Lagrange’s theorem says if H is a subgroup of G
then O(H) | 0(G).
So 0(H) can be 1, 5, 7 or 35.
So largest subgroup size other than G itself is 7.
![]()
Question 96.
A relation R is said to be circular if aRb and bRc together imply cRa.
Which of the following options is/are correct?
(a) If a relation S is reflexive and circular, then S is an equivalence relation.
(b) If a relation S is circular and symmetric, then S is an equivalence relation.
(c) If a relation S is transitive and circular, then S is an equivalence relation.
(d) If a relation S is reflexive and symmetric, then S is an equivalence relation.
Answer/Explanation
Answer: (a) If a relation S is reflexive and circular, then S is an equivalence relation.
Explanation:
Let S be reflexive and circular,
Let us checking symmetry:
Symmetry:
Let xSy
Now since S is reflexive ySy true.
So xSy and ySy is true
Now by circular property we get, ySx
So xSy => ySx
So S is symmetric.
Transitive:
Let xSy and ySz
Now by circular property we get zSx and by symmetry property proved above, we get
zSx => xSz
So xSy and ySz => xSz
So S is transitive.
So S is reflexive, symmetric and transitive and hence an equivalence relation.
So option (a) is true.
Option (b): Let S be circular and symmetric. Let S be defined on set {1, 2, 3}
Now empty relation is circular and symmetric but not reflexive. So S need not be an equivalence relation.
So option (b) is false.
Option (c): Let S be transitive and circular. Let S be defined on the set {1, 2, 3}
Now empty relation again satisfies transitive and circular but is not reflexive. So S need not be an equivalence relation.
So option (c) is false.
Option (d): Reflexive and symmetric need not be transitive for example on {1, 2, 3}.
S = {(L 1), (2, 2), (3, 3), (1, 2), (2, 1), (2, 3), (3, 2)}
is reflexive and symmetric. But it is not transitive because (1, 2) and (2, 3) belong to S but (1, 3) does not.
So option (d) is false.
Question 97.
Let G be a group of order 6, and Hbe a subgroup of G such that 1 < | H | <6. Which one of the following options is correct?
(a) Both G and H are always cyclic.
(b) G is always cyclic, but H may not be cyclic.
(c) G may not be cyclic, but H is always cyclic.
(d) Both G and H may not be cyclic.
Answer/Explanation
Answer: (c) G may not be cyclic, but H is always cyclic.
Explanation:
|G| = 6
H is subgroup, so by Lagrange’s theorem
| H | = 1, 2, 3 or 6 (Divisor’s of 6) Now it is given that 1 < | H | <6 or | H | = 2 or 3
Since 2 and 3 are both prime and since every group of prime order is cyclic, H is surely cyclic. But order of | G | =6 which is not prime. So G may or may not be cyclic. So G may not be cyclic, but H is always cyclic. Option (c) is correct.
Question 98.
Consider the following sets, where n ≥ 2:
S1: Set of all n × n matrices with entries from the set {a, b, c}
S2: Set of all functions from the set {0,1, 2, n2 – 1} to the set {0, 1, 2}
Which of the following choice(s) is/are correct?
(a) There exists a surjection from S1 to S2.
(b) There does not exist a bijection from S1 to S2.
(c) There does not exist an injection from S1 to s2.
(d) There exists a bijection from S1 to S2.
Answer/Explanation
Answer:
(a) There exists a surjection from S1 to S2.
(d) There exists a bijection from S1 to S2.
Explanation:
| S1 | = 3n
Since each of the n2 entries in n × n matrix can be fills in 3 ways.
|S2| = 3n2
Since | {0, 1, 2} | =3 and | {0, 1, 2, n2 — 1} | = n2)
Now the theorem says A bijection fA → B exists iff |A| = |B|.
Here |S1| = |S2|
So, there has to be a bijection from S1 to S2. So, option (d) is correct. If bijection exists surely surjection also exists. So, option (a) is also correct. Option (b) and (c) are incorrect.
Question 99.
Let S be a set consisting of 10 elements. The number of tuples of the form (A, B) such that A and B are subsets of S and A ⊆ B is _______.
Answer/Explanation
Explanation:
The Venn diagram for this is
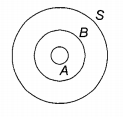
Now every element x in S has only 3 options. It can be x ∈ A or x ∈ B – A or x ∈ S — B. So the number of ways to choose A and B such that A ⊆ B ⊆ S is 310.
![]()
Question 100.
For two n-dimensional real vectors P and Q, the operation s(P, Q) is defined as follows:
s(P, Q) = \(\sum_{i=1}^{n}\)(P[i].Q[i])
Let L be a set of 10-dimensional non-zero real vectors such that for every pair of distinct vectors P, Q ∈ L, s(P, Q) = 0. What is the maximum cardinality possible for the set L?
(a) 10
(b) 9
(c) 100
(d) 11
Answer/Explanation
Answer: (a) 10
Explanation:
L is the set of 10-dimensional orthogonal vectors.
So cardinality of L ≤ 10.
i.e., Maximum cardinality of L = 10.
So, option (a) is correct.
