Computer Science Mathematical Logic MCQ Quiz Questions and Answers PDF Download
![]()
Question 1.
Indicate which of the following well-formed formula are valid:
(a) ((P⇒Q) ∧ (Q ⇒ R)) ⇒ (P ⇒ R)
(b) (P ⇒ Q) ⇒(¬ P ⇒ ¬ Q)
(c) (P∧(¬P V¬ Q)) ⇒ Q
(d) ((P ⇒ R) ∨ (Q ⇒ R)) ⇒ ((P ∨ Q)) ⇒ R)
Answer/Explanation
Answer: (a) ((P ⇒ Q) ∧ (Q ⇒ R)) ⇒ (P ⇒ R)
Explanation:
Option (a) is well known valid formula (tautology) because it is a rule of inference called a hypothetical syllogism. By applying Boolean algebra and simplifying, we can show that (b), (c), and (d) are invalid.
For example,
Choice (b) ≡(P ⇒ Q) ⇒ (¬P ⇒ ¬Q)
≡(P ⇒ Q) ⇒ (P ⇒Q’)
≡(P’ + Q) ⇒ (P + Q’)
≡(P’ + Q)’ + (P+Q’)
≡PQ’ + P+Q’
≡P+ Q’
≠1
So, invalid.
Question 2.
Which of the following predicate calculus statements is/are valid
(a) (∀x) P(x)∨ (∀x) Q(x) → (∀x) {P(x) ∨ Q(x)}
(b) (∃x) P(x) ∧ (∃x) Q(x) → (∃x) {P(x) ∧ Q(X)}
(c) (∃x) {P(x) ∨ Q(x)} → (∀x) P(x) ∨ (∀x) Q(x)
(d) (∃x) {P(x) ∨ Q(x)} → ∃x P(x) ∨ ∀x Q(x)
Answer/Explanation
Answer: (a) (∀x) P(x)∨ (∀x) Q(x) → (∀x) {P(x) ∨ Q(x)}
Explanation:
According to distributive properties
∀x (P(x) ∧ Q(x)) ↔ ∀xP(x) ∧ ∀xQ(x)
(∀xP(x) ∨∀xQ(x)) → ∀x(P(x) ∨ Q(x))
∃x (P(x) ∨ Q(x)) ↔ ∃xP(x)∨∃xQ(x)
∃x(P(x) ∧Q(X)) → ∃xP(x) ∧∃xQ(X)
So option (a) is valid.
Question 3.
Which of the following is/are tautology:
(a) (a ∨ b) → (b ∧ c)
(b) (a ∧ b) → (b ∨ c)
(c) (a ∨ b) → (b → c)
(d) (a → b) → (b → c)
Answer/Explanation
Answer: (b) (a ∧ b) → (b ∨ c)
Explanation:
(a) (a ∨ b) → (b ∧ c)
≡ (a + b)’ + bc
≡ a’b’+ bc
Therefore, ((a ∨ b) → (b ∧ C)) is contingency and not tautology.
(b) (a ∧ b) → (b ∨ c)
≡ ab → b + c
≡ (ab)’ + b + c
≡a’ + b’ + b + c
≡a’ + 1 + c
≡1
So ((a ∧b) → (b ∨c)) is tautology.
(c) (a ∨ b) → (b → c)
≡ (a + b) → (b’ + c)
≡(a +b)’ +b’ + c
≡a’b’ + b’ + c
≡b’ + c
So ((a ∨b) → (b → c)) is contingency but not a tautology.
(d) (a → b) → (b → c)
≡(a’ + b) → (b’ + c )
≡(a’ + b)’ + b’ + c
≡ ab’ + b’ + c
≡b’ + c
Therefore, ((a → b) → (b → c)) is contingency but not tautology.
![]()
Question 4.
The proposition p ∧ (~p ∨ q) is
(a) A tautology
(b) ⇔ (p ∧ q)
(c) ⇔ (p ∨ q)
(d) A Contradiction
Answer/Explanation
Answer: (b) ⇔ (p ∧ q)
Explanation:
The proposition p ∧ (~p ∨ q)
≡p(p’ + q) ≡pq
≡p ∧ q
Question 5.
Let p and q be propositions. Using only the truth table decide whether p ⇔ q does not imply p →¬ q is true or false.
Answer/Explanation
Answer: TRUE
Explanation:
| p | q | P ↔ q | P → ~ q | (p ↔ q) → (p → ~ q) |
| T | T | T | F | F |
| T | F | F | T | T |
| F | T | T | T | T |
| F | F | F | T | T |
From the truth table, (p ↔ q) → (p → ~q) is not a tautology, hence it is true that p ↔ q doesn’t imply p →¬q.
Question 6.
If the proposition ¬ p ⇒ q is true, then the truth value of the proposition ¬ p ∨ (p ⇒ q), where ¬ is negation, ‘∨’ is inclusive or and ‘⇒’ is the implication, is
(a) True
(b) Multiple valued
(c) False
(d) Cannot be determined
Answer/Explanation
Answer: (d) Cannot be determined
Explanation:
| P | q | ¬ p → q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Now since ¬p → q is given true, We reduce the truth table as follows.
| p | q | ¬ p → q |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
In the reduced truth table we need to find the true value of ¬p ∨(p → q) ≡p’ +(p → q) ≡p’ + p’ +q ≡p’ + q
The truth value of p’ + q in the reduced truth table is given below.
| P | q | P’ + q |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Since in the reduced truth table also, the given expression is sometimes true and sometimes false, therefore the truth value of proposition ¬p ∨(p → q) can not be determined.
Question 7.
Which one of the following is false? Read ∧ as AND, ∨ as OR, ~ as NOT, → as one-way implication, and ↔ as two-way implication.
(a) ((x → y) ∧ x) → y
(b) ((~ x → y) ∧ (~ x → ~ y) ) → x
(c) (x → (x ∨ y))
(d) ((x ∨ y)↔(~ x → ~ y))
Answer/Explanation
Answer: (d) ((x ∨ y)↔(~ x → ~ y))
Explanation:
(d) ((x ∨y) ↔ (~x →~y))
= (x ∨ y) ↔ (~(~x ) ∨~y)
= (x ∨ y) ↔ (~x ∨~y)
= ((x ∨ y) ∧ (~x ∨~y)) ∨(~(x ∨y) ∧~(x ∨~y))
= ((x ∨(y ∧ ~y)) ∨(( ~x ∧ ~y) ∧ (~x ∧ y))
= (x ∨ F) ∨ ((~x ∧ ~y) ∧(~x ∧ y))
= x ∨ (~x ∧(y ∧~y)) = x ∨(~x ∧F)
= x ∨ F = x
![]()
Question 8.
Let a, b, c, d be propositions. Assume that the equivalence a ↔ (b ∨ ¬ b) and b ↔ c hold. Then the truth-value of the formula (a ∧ b) → (a ∧ c) ∨ d is always
(a) True
(b) False
(c) Same as the truth-value of b
(d) Same as the truth-value of d
Answer/Explanation
Answer: (a) True
Explanation:
. a ↔ (b ∨¬b)
a ↔ True
So a is true, i.e. a = 1
. b ↔ c holds. So b = c
Now the given expression is
(a ∧ b) → ((a ∧ c) ∨d) ≡(a . b) → ((a . c) + d)
putting a=1 in above expression We get
1 . b →((1 . c) +d)
≡ b → c + d
≡ b’ + c + d
Now putting b=c in above expression We get
≡c’ + c + d ≡1 + d ≡1
So the expression is always true.
Question 9.
What is the converse of the following assertion? I stay only if you go
(a) I stay if you go
(b) If I stay then you go
(c) If you do not go then I do not stay
(d) If I do not stay then you go
Answer/Explanation
Answer: (a) I stay if you go
Explanation:
Let p: I stay
q: you go
I stay only if you go
p → q
The converse of p → q is q → p
Now convert the answers one-by-one into boolean form. Only option (a) i.e. “I stay if you go” converts to q → p.
Question 10.
Consider two well-formed formulas in propositional logic:
F1: P ⇒ ¬ P
F2: (P ⇒ ¬ P) v ( ¬ P ⇒P)
Which of the following statements is correct?
(a) F1 is satisfiable, F2 is valid
(b) F1 is unsatisfiable, F2 is satisfiable
(c) F1 is unsatisfiable, F2 is valid
(d) F1 and F2 are both satisfiable
Answer/Explanation
Answer: (a) F1 is satisfiable, F2 is valid
Explanation:
F1: P → ~P ≡ p → p’ ≡ p’ + p’ ≡p’
So F1 is contingency. Hence, F1 is satisfiable but not valid.
F2: (P → ~P) ∨ (~P → P)
≡ (p → p’) + (p’ → p)
≡ (p’+p’) + (p + p)
≡ p’ + p ≡ 1
So F2 is tautology and therefore valid.
Question 11.
“If X then Y unless Z” is represented by which of the following formulas in propositional logic? (“¬”) is negation, “ ∧” is the conjunction, and “→” is the implication)
(a) (X ∧¬ Z) → Y
(b) (X ∧ Y) → ¬ Z
(c) X → (Y ∧ ¬ Z)
(d) (X → Y) ∧ ¬ Z
Answer/Explanation
Answer: (a) (X ∧¬ Z) → Y
Explanation:
If X then Y unless Z is represented by
X →Y unless Z ≡ (X → Y) + Z
≡ X’ + Y + Z
Now convert the answers one-by-one into boolean form only choice (a) converts to X’+ Y+ Z as can be seen below:
(X∧~Z) →Y ≡ XZ’ → Y
≡ (XZ’)’ + y
= X’+ Y+Z
![]()
Question 12.
Which of the following is a valid first order formula? (Here α and β are first order formulae with x as their only free variable)
(a) ((∀x) [α] ⇒ (∀x)[β]) ⇒ (∀x) [α ⇒ β]
(b) (∀x) [α] ⇒ (∃x) [α ∧ β]
(c) (∀x) [α v β ] ⇒ (∃x) [α] ⇒ (∀x) [α]
(d) (∀x) [α ⇒ β ] ⇒ ((∀x) [α] ⇒ (∀x) [β])
Answer/Explanation
Answer: (d) (∀x) [α ⇒ β ] ⇒ ((∀x) [α] ⇒ (∀x) [β])
Explanation:
(∀x) [α ⇒ β] ⇒ ((∀x) [α] ⇒ ∀(x) [[β]) is a logical equivalence and therefore, a valid first order formula.
Question 13.
Consider the following formula α and its two interpretations I1 and I2.
α : (∀x) [Px ⇔ (∀y) [Qxy ⇔ ¬ Qyy]] ⇒ (∀x)[¬ Px]
I1 : Domain: the set of natural numbers
Px ≡ ‘x is a prime number ‘
Qxy ≡’y divides x’
I2: Same as I1 except that Px = ‘x is a composite number.’
Which of the following statements is true?
(a) I1 satisfies α, I2 does not
(b) I2 satisfies α, I1 does not
(c) Neither I2 nor I1 satisfies α
(d) Both I1 and I2 satisfy α
Answer/Explanation
Answer: (d) Both I1 and I2 satisfy α
Explanation:
Qxy ≡ “y divides y” is always true
∴Qxy ⇔ ¬ Qxy is the same as Qxy ⇔False
Now α becomes
(∀x)[P(x)⇔(∀y)(Qxy⇔false)]
⇒ (∀x) [¬ P(x)]
Now consider I1: P(x) = “x is a prime number”. α becomes
(∀x x is a prime number if and only if ∀y (y does not divide x)) ⇒ (∀x) x is not prime. which means that x is a prime number if and only if no number divides x implies that no number is prime. Since x always divides x, the above sentence is true.
Now consider I2: P(x) = “x is a composite number”. Now α becomes
(∀x x is a composite number if and only if ∀y (y does not divide x)) ⇒ (∀x) x is not composite. This means that x is a composite number if and only if no number divides x implies that no number is composite.
Since x always divides x, the above sentence is true.
∴ Both I1 and I2 satisfy α.
Question 14.
The following resolution rule is used in logic programming: Derive clause (P ∨ Q) from clauses (P ∨ R), (Q ∨ ¬ R) Which of the following statements related to this rule is FALSE?
(a) (P ∨ R)∧(Q ∨ ¬ R) ⇒ (P ∨ Q) is logically valid
(b) (P ∨ Q) ⇒ (P ∨ R) ∧ (Q ∨¬ R) is logically valid
(c) (P ∨ Q) is satisfiable if and only if (P ∨ R) ∧ (Q ∨ ¬ R) is satisfiable
(d) (P ∨ Q) ⇒ FALSE if and only if both P and Q are unsatisfiable
Answer/Explanation
Answer: (b) (P ∨ Q) ⇒ (P ∨ R) ∧ (Q ∨¬ R) is logically valid
Explanation:
Derive clause P ∨ Q from clauses P ∨ R, Q ∨¬R means that (P ∨ R) ∧ (Q ∨ ¬R) ⇒ P ∨ Q
.’. (a) is true
Since x ⇒ y does not imply that y ⇒ x
.’. P ∨ Q ⇒ (P ∨ R) ∧ (Q ∨¬R)
.’. may or may not be true.
Hence (b) is false.
Question 15.
Identify the correct translation into the logical notation of the following assertion. Some boys in the class are taller than all the girls
Note: Taller (x, y) is true if x is taller than y.
(a) (∃x) (boy(x) → (∀y) (girl(y) ∧ taller (x, y)))
(b) (∃x) (boy(x) ∧ (∀y) (girl(y) ∧ taller (x, y)))
(c) (∃x) (boy(x) → (∀y) (girl(y) → taller (x, y)))
(d) (∃x) (boy(x) ∧ (∀y) (girl(y) → taller (x, y)))
Answer/Explanation
Answer: (d) (∃x) (boy(x) ∧ (∀y) (girl(y) → taller (x, y)))
Explanation:
The statement is “some boys in the class are taller than all the girls”. so the notation for the given statement is (∃x) (boy(x) ∧(∀y) (girl(y) → taller (x,y)))
Question 16.
Let an (x, y), b(x, y,), and c(x, y) be three statements with variables x and y chosen from some universe. Consider the following statement:
(∃x)(∀y)[(a(x,y) ∧ b(x,y)) ∧ ¬ c(x,y)]
Which one of the following is its equivalent?
(a) (∀x)(∃y)[(a(x,y) ∨ b(x,y)) ∧ ¬ c(x,y)]
(b) (∃x)(∀y)[(a(x,y) ∨ b(x,y)) ∧ ¬ c(x,y)]
(c) ¬(∀x)(∃y)[(a(x,y) ∧ b(x,y)) → c(x,y)]
(d) ¬ (∀x)(∃y)[(a(x,y) ∨ b(x,y)) → c(x,y)]
Answer/Explanation
Answer: (c) ¬(∀x)(∃y)[(a(x,y) ∧ b(x,y)) → c(x,y)]
Explanation:
Choice (c) is
¬(∀x)(∃y)[(a(x,y) ∧ b(x,y)) → c(x,y)]
= ¬(∀x)(∃y)[a ∧ b → c]
= ¬(∀x)(∃y)[(ab)’ + c]
= ∃x ∀y[(ab)’ + c]’
= ∃x ∀y [abc’] = ∃x ∀y [a ∧ b ∧ ¬C] which is same as the given expression. (∃x)(∀y)[(a(x,y) ∧ b(x,y)) ∧ ¬c(x,y)]
![]()
Question 17.
Let p, q, r, and s be four primitive statements. Consider the following arguments:
P: [(¬ p ∨ q) ∧ (r → s) ∧ (p ∨ r)] → (¬ s → q)
Q: [(¬ p ∧ q) ∧ [q → (p → r)]] → ¬ r
R: [[(q ∧ r) → p] ∧ (¬q ∨ p)] → r
S: [p ∧ (p → r) ∧ (q ∨ ¬ r)] → q
Which of the above arguments are valid?
(a) P and Q only
(b) P and R only
(c) P and S only
(d) P, Q, R, and S
Answer/Explanation
Answer: (c) P and S only
Explanation:
p: [(¬p ∨q) ∧(r → s) ∧(p ∨r)] →q
≡p(p’ +r)(q + r’) →q
≡pr(q +r’) →q
≡prq →q
≡(prq)’ + q
≡p’ + r’ + q’ + q
≡p’ + r’ + 1
≡1
Therefore S is valid.
Q and R can be similarly simplified in boolean algebra to show that is both not equivalent to 1.
Question 18.
The following propositional statement is
(P →(Q ∨ R)) → ((P ∧ Q) → R)
(a) Satisfiable but not valid
(b) Valid
(c) A contradiction
(d) None of the above
Answer/Explanation
Answer: (a) Satisfiable but not valid
Explanation:
(p → (Q ∨R)) → ((P ∧Q) → R)
≡(P → Q + R) → (PQ → R)
≡[P’ + Q + R] → [(PQ)’ + R]
≡[P’ + Q + R] → [P’ + Q’ + R]
≡(P’ + Q + R)’ + P’ + Q’ + R
≡P Q’ R’ + P’ + Q’ + R
≡Q’ + Q’ P R’ + P’ + R
≡Q’ + P’ + R (by absorption law)
which is a contingency (i.e. satisfiable but not valid).
Question 19.
Let P, Q, and R be three atomic propositional assertions. Let X denote (P ∨ Q) → R and Y denote (P → R) ∨ (Q → R). Which one of the following is a tautology?
(a) X ≡ Y
(b) X → Y
(c) Y → X
(d) ¬ Y →X
Answer/Explanation
Answer: (b) X → Y
Explanation:
X: (P ∨ Q) → R
Y: (P → R) ∨(Q → R)
X: P + Q → R ≡(P + Q)’ + R ≡P’ Q’ + R
Y: (P’ + R) + (Q’ +R) ≡P’ + Q’ + R
Clearly X ≠ Y
Consider X → Y
≡(P’Q’ +R) →(P’ + Q’ + R)
≡(P’Q’+R)’ + P’ + Q’ + R
≡(P’Q’)’ . R’ + P’ + Q’ + R
≡(P + Q) . R’ + P’ + Q’ + R
≡ PR’ + QR’ + P’ + Q’ + R
≡ (PR’ + R) + (QR’ + Q’) + P’
≡(P + R) (R’ + R) + (Q + Q’) × (R’ +Q’) + P’
≡(P + R) + (R’ + Q’) + P’
≡P + P’ + R + R’ + Q’
≡1 + 1 + Q’
≡ 1
∴X → Y is a tautology.
![]()
Question 20.
What is the first order predicate calculus statement equivalent to the following? Every teacher is liked by some student
(a)∀(x) [teacher (x) → ∃ (y) [student (y) → likes (y, x)]]
(b)∀(x) [teacher (x) → ∃ (y) [student (y) ∧ likes (y, x)]]
(c) ∃(y) ∀(x) [teacher (x) → [student (y) ∧ likes (y, x)]]
(d) ∀(x) [teacher (x) ∧ ∃(y) [student (y) → likes (y, x)]]
Answer/Explanation
Answer: (b)∀(x) [teacher (x) → ∃ (y) [student (y) ∧ likes (y, x)]]
Explanation:
Every teacher is liked by some student: then the logical expression is ∀(x) [teacher(x) → ∃(y) [student (y) ∧ likes (y, x)]] Where likes (y, x) means y likes x, such that y represent the student and x represents the teacher.
Question 21.
Let P(x) and Q(x) be arbitrary predicates. Which of the following statements is always TRUE?
(a) (∀x(P(x) ∨ Q(x))) ⇒ ((∀xP(x)) ∨ (∀xQ(x)))
(b) (∀x(P(x) ⇒ Q(x))) ⇒ ((∀xP(x)) ⇒ (∀xQ(x)))
(c) (∀x(P(x) ⇒ (∀xQ(x)))) ⇒ (∀x(P(x) ⇒ Q(x)))
(d) ((∀x(P(x)) ⇔ (∀xQ(x))) ⇒ (∀x(P(x) ⇔ Q(x)))
Answer/Explanation
Answer: (b) (∀x(P(x) ⇒ Q(x))) ⇒ ((∀xP(x)) ⇒ (∀xQ(x)))
Explanation
Consider choice (b)
(∀x(P(x) ⇒ Q(x))) ⇒ ((∀xP(x)) ⇒ (∀xQ(x))) Let the LHS of this implication be true This means that
P1 → Q1
p2 → Q2
.
.
.
Pn → Qn
Now we need to check if the RHS is also true. The RHS is ((∀xP(x)) ⇒ (∀xQ(x)))
To check this let us take the LHS of this as true i.e. take∀xP(x) to be true. This means that (P1 P2,…Pn ) is taken to be true. Now P1 along with P1 → Q1 will imply that is true. Similarly
P2 along with P2 → Q2, will imply that Q2 is true. And so on…
Therefore (Q1, Q2,……Qn) all true.
i.e. ∀x Q(x) is true. Therefore statement (b) is a valid predicate statement.
Question 22.
Consider the following first-order logic formula in which R is a binary relation symbol.
∀x ∀y ( R(x,y) ⇒ R(y, x))
The formula is
(a) Satisfiable and valid
(b) Satisfiable and so is its negation
(c) Unsatisfiable but its negation is valid
(d) Satisfiable but its negation is unsatisfiable
Answer/Explanation
Answer: (b) Satisfiable and so is its negation
Explanation:
Since a relation may or may not be symmetric, the given predicate is satisfiable but not valid. So (a) is clearly false.
Whenever a predicate is satisfiable its negation also is satisfiable. So option (b) is the correct answer.
Question 23.
Which one of the first-order predicate calculus statements given below correctly expresses the following English statement?
Tigers and lions attack if they are hungry or threatened.
(a) ∀x [(tiger (x) ∧ lion (x)) → {(hungry (x) ∨ threatened (x)) → attacks (x)}]
(b) ∀x [(tiger (x) ∨ lion (x)) → {(hungry (x) ∨ threatened (x)) ∧ attacks (x)}]
(c) ∀x [(tiger (x) ∨ lion (x)) → {(attacks (x) → (hungry (x) ∨ Threatened (x))}]
(d) ∀x [(tiger (x) ∨ lion (x)) → {(hungry (x) ∨ threatened (x)) → attacks (x)}]
Answer/Explanation
Answer: (d) ∀x [(tiger (x) ∨ lion (x)) → {(hungry (x) ∨ threatened (x)) → attacks (x)}]
Explanation:
The given statement should be read as “If an animal is a tiger or a lion, then (if the animal is hungry or threatened, then it
will attack). Therefore the correct translation is ∀x [(tiger (x) ∨ lion (x)) → {(hungry (x) ∨ threatened (x)) → attacks (x)}] which is choice (d).
![]()
Question 24.
Consider the following propositional statements:
P1: ((A ∧ B) → C)) ≡ ((A → C) ∧(B → C))
P2: ((A ∨ B) → C)) ≡ ((A → C) ∨ (B → C))
Which one of the following is true?
(a) P1 is a tautology, but not P2
(b) P2 is a tautology, but not p1
(c) P1 and P2 are both tautologies
(d) Both P1 and P2 are not tautologies
Answer/Explanation
Answer: (d) Both P1 and P2 are not tautologies
Explanation:
P1: ((A ∧ B) → c) ≡ ((A → c) ∧ (B → c))
LHS :
(A ∧ B) → C
≡ AB → C
≡ (A B)’ + C
≡ A’ + B’ + C
RHS:
(A → C) ∧ (B → C)
≡ (A’+ C) (B’ + C)
≡ A’B’ + C
Clearly, LHS ≠ RHS
P1 is not a tautology
P2: ((A ∨ B → C)) ≡ ((A → C) ∨(B → C))
LHS ≡ (A + B → C)
≡ (A + B)’+C
≡ A’B’ + C
RHS = (A → C) ∨ (B → C)
≡ (A’+ C) + (B’ + C)
≡ A’+ B’ + C
Clearly, LHS ≠ RHS ⇒ P2 is also not a tautology. Therefore, both P1 and P2 are not tautologies. The correct choice is (d).
Question 25.
A logical binary relation ⊙ is defined as follows:
| A | B | A ⊙ B |
| True | True | True |
| True | False | True |
| False | True | False |
| False | False | True |
Let ~ be the unary negation (NOT) operator, with higher precedence, than ⊙. Which one of the following is equivalent to A ∧ B?
(a) (~ A ⊙ B)
(b) ~ (A ⊙ ~ B)
(c) ~ (~ A ⊙ ~ B)
(d) ~ (~ A ⊙ B)
Answer/Explanation
Answer: (d) ~ (~ A ⊙ B)
Explanation:
By using min terms we can define
A⊙B = AB + AB’ + A’B’
= A + A’B’
= (A + A’) . (A + B’) = A + B’
(a) ~ A⊙B = A’⊙ B = A’ + B’
(b) ~ (A ⊙ ~B) = (A ⊙ B’)’ =(A + (B’)’)’
= (A + B)’ = A’B’
(c) ~ (~A ⊙ ~B) = (A’ ⊙ B’)’ = (A’ + (B’)’)’
= (A’ + B)’ = AB’
(d) ~ (~A ⊙ B) = (A’ ⊙ B)’ = (A’ + B’)’
= A . B = A ∧ B
∴ Only, choice (d) = A ∧ B
Note: This problem can also be done by constructing a truth table for each choice and comparing it with the truth table for A ∧ B.
Question 26.
Let Graph (x) be a predicate that denotes that x is a graph. Let Connected (x) be a predicate that denotes that x is connected. Which of the following first-order logic sentences DOES NOT represent the statement; “Not every graph is connected”?
(a) ¬∀x (Graph(x) ⇒ Connected (x))
(b) ∃x (Graph(x) ∧¬ Connected (x))
(c) ¬∀x (¬ Graph(x) ∨ Connected (x))
(d) ∀x (Graph(x) ⇒ ¬ Connected (x))
Answer/Explanation
Answer: (d) ∀x (Graph(x) ⇒ ¬ Connected (x))
Answer:
Explanation:
The statement “Not every graph is connected” is the same as “There exists some graph which is not connected” which is the same as
∃x {graph (x) ∧ ¬ connected (x)}
Which is choice (b)
By boolean algebra, we can see that options (a) and (c) are the same as (b). Only option (d) is not the same as (b).
In fact option (d) means that “all graphs are not connected”.
Alternate solution:
We can translate the given statement “NOT (every graph is connected)” as ¬(∀x graph (x) → connected (x))
≡∃x¬(graph (x) →connected (x))
≡ ∃x¬(¬graph (x) ∨connected (x))
≡ ∃x (graph (x) ∧ ¬ connected (x))
By boolean algebra, we can see that options (a) and (c) are the same as (b). Only option (d) is not the same as (b).
In fact option (d) means that “all graphs are not connected”.
![]()
Question 27.
Which of the following is TRUE about formulae in Conjunctive Normal Form?
(a) For any formula, there is a truth assignment for which at least half the clauses evaluate to true.
(b) For any formula, there is a truth assignment for a which all the clauses evaluate to true.
(c) There is a formula such that for each truth assignment at most one-fourth of the clauses evaluate to true.
(d) None of the above
Answer/Explanation
Answer: (a) For any formula, there is a truth assignment for which at least half the clauses evaluate to true.
Explanation:
In conjunction normal form, for any particular assignment of truth values, all except one clause, will always evaluate to true. So, the proportion of clauses which evaluate to true to the total
number of clauses is equal to \(\frac{2^{n}-1}{2^{n}}\)
Now putting n = 1, 2, . . . . ., We get \(\frac{1}{2}\) , \(\frac{3}{4}\) , \(\frac{7}{8}\) ….
All of these proportions are ≥ \(\frac{1}{2}\) and so choice (a) at least half of the clauses evaluate to true, is the correct answer.
Question 28.
Which one of these first-order logic formulae is valid?
(a) ∀x(P(x) ⇒ Q(x)) ⇒ ((∀xP(x)) ⇒ (∀xQ(x)))
(b) ∃x(P(x) ∨ Q(x)) ⇒ ((∃xP(x)) ⇒ (∃xQ(x)))
(c) ∃x(P(x) ∧ Q(X)) ⇔ ((∃xP(x)) ∧ (∃xQ(x)))
(d) ∀x∃y P(x, y) ⇒ ∃y∀xP(x, y)
Answer/Explanation
Answer: (a) ∀x(P(x) ⇒ Q(x)) ⇒ ((∀xP(x)) ⇒ (∀xQ(x)))
Explanation:
Option (a) is a standard one-way distributive property of predicates.
Question 29.
Let fsa and pda be two predicates such that fsa(x) means x is a finite state automaton and pda(y) means, that y is a pushdown automaton. Let equivalent be another predicate such that equivalent (a, b) means a and b are equivalent. Which of the following first-order logic statement represents the following:
Each finite state automaton has an equivalent pushdown automaton.
(a) ∀x (fsa(x) ⇒ ∃y (pda(y) ∧ equivalent (x, y)))
(b) ~∀y(∃x fsa(x) ⇒ pda(y) ∧ equivalent (x, y))
(c) ∀x ∃y (fsa(x) ∧ pda(y) ∧ equivalent (x, y))
(d) ∀x ∃y (fsa{y) ∧ pda(x) ∧ equivalent (x, y))
Answer/Explanation
Answer: (a) ∀x (fsa(x) ⇒ ∃y (pda(y) ∧ equivalent (x, y)))
Explanation:
“For x which is a fsa, there exists a y which is a pda and which is equivalent to x.” ∀x (fsa(x) ⇒ ∃y (pda(y) ∧ equivalent (x, y))) is the logical representation.
Question 30.
Which of the following first order formulae is logically valid? Here a(x) is a first order formula
(a) [β → (∃x,α(x))] → [∀x, β → α(x)]
(b) [∃x, β → α(x)] → [β → (∀x, α(x))]
(c) [(∃x, α(x)) → β] → [∀x,α(x) → β]
(d) [(∀x,α(x)) → β] → [∀x, α(x) → β]
Answer/Explanation
Answer: (c) [(∃x, α(x)) → β] → [∀x,α(x) → β]
Explanation:
Option (c) is [(∃x, α(x)) → β] → [∀x,α(x) → β] Let us check the validity of this predicate. Let the LHS of this predicate be true.
This means that some α → β.
Let a5 → β
Now we will check if the RHS is true. The RHS is [∀x,α(x) → β] to check this implication let us take ∀x,α(x)to be true.
This means that all the a are true. It means that a5 is also true.
But α5 → β. Therefore β is true.
So the RHS [∀x,α(x) → β] is true.
Whenever the LHS [(∃x, α(x)) → β] is true. So option (c) is valid.
![]()
Question 31.
Which of the following is the negation of [(∀x,α → (∃y, β → (∀u,∃v,y))]
(a) [∃x,α → (∀y,β → (∃u,∀u, Y))]
(b) [∃x,α →(∀y,β → (∃u,∀u, ¬ Y))]
(c) [∀x,¬α → (∃y,¬β →(∀u,∃u ¬Y))]
(d) [∀x,α ∧ (∃y, β ∧ (∃U, ∀U, ¬Y))]
Answer/Explanation
Answer: (d) [∀x,α ∧ (∃y, β ∧ (∃U, ∀U, ¬Y))]
Explanation:
The given predicate is
[∀x, α → (∃y,β → (∀u, ∃u, y))]
The negation is of this predicate is
¬[∀x, α → (∃y,β → ∀u, ∃u, y)]
¬[∀x, α →(∀y, ¬β ∨∀u, ∃u, y)]
¬[∃x, ¬α ∨(∀y, ¬β ∨∀u, ∃u, y)]
[∀x, α ∧ (∃y, β ∧(∃y, β ∧ (∃u, ∀u, ¬y))]
which is an option (d).
Question 32.
P and Q are two propositions, which of the following logical expressions are equivalent?
1. P ∨ ~Q
2. ~ (~P ∧ Q )
3. (P ∧ Q) ∨ (P ∧ ~Q) ∨ (~P ∧ ~ Q)
4. (P ∧ Q) ∨ (P ∧ ~Q) ∨ (~P ∧ Q)
(a) Only 1 and 2
(b) Only 1, 2 and 3
(c) Only 1, 2 and 4
(d) All of these
Answer/Explanation
Answer: (b) Only 1, 2 and 3
Explanation:
1. P ∨ ~Q ≡ P + Q’
2. ~(~P ∧ Q) ≡ (P’Q)’ ≡P+Q’
3. (P ∧ Q) ∨ (P ∧ ~Q) ∨ (~P ∧ ~Q)
≡ PQ + PQ’ + P’Q’
≡ P(Q + Q’) + P’Q’
≡ P + P’Q’
≡ (P + P’) (P + Q’)
≡ P + Q’
4. (P ∧ Q) ∨ (P ∧ ~Q) ∨ (~P ∧ Q)
≡ PQ + PQ’ + P’Q
≡ P(Q + Q’) + P’Q
≡ P + P’Q
≡ (P + P’) (P + Q) = P + Q
Clearly (i), (ii) and (iii) are equivalent. Correct choice is (b).
Question 33.
Which one of the following is the most appropriate logical formula to represent the statement: “Gold and silver ornaments are precious”
The following notations are used:
G(x): x is a gold ornament
S(x): x is a silver ornament
P(x): x is precious
(a) ∀x(P(x) → (G(x) ∧ S(x)))
(b) ∀x(G(x) ∧ (S(x) → P(x)))
(c) ∃x((G(x) ∧ S(x)) → P(x))
(d) ∀x ((G(x) ∨ S(x)) → P(x))
Answer/Explanation
Answer: (d) ∀x ((G(x) ∨ S(x)) → P(x))
Explanation:
The correct translation of “Gold and silver ornaments are precious” is choice (d)
∀x((G(x) ∨ S(x)) → P(x))
which is read as “if an ornament is a gold or silver, then it is precious”. Now since a given ornament cannot be both gold and silver at the same time.
Choice (b) ∀x ((G(x) ∧ S(X)) → P(x)) is incorrect.
Question 34.
The binary operation □ is defined as follows:
Table
Which one of the following is equivalent to P ∨ Q?
(a) ¬Q □ ¬ P
(b) P □ ¬ Q
(c) ¬P □ Q
(d) ¬ P □ ¬ Q
Answer/Explanation
Answer: (b) P □ ¬ Q
Explanation:
The given table can be converted into a boolean function by adding minterms corresponding to true rows.
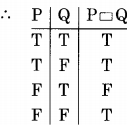
Since there is only one false in the above truth table, we can represent the function P □ Q more efficiently, in conjunctive normal form. Translates P □ Q = P + Q’ (the max-term corresponding to the third row, where the function is false).
Now, we can easily translate the choices into boolean algebra as follows:
Choice (a) ¬Q □ ¬P ≡ Q’ □ P’ ≡ Q’ + P
Choice (b) P □ ¬Q ≡ P □ Q’ ≡ P + Q
Choice (c) ¬P □ Q ≡ P’ □ Q ≡ P’ + Q’
Choice (d) ¬P □ ¬Q ≡ P’ □ Q’ ≡ P’ + Q
As we can clearly see only choice (b) P □ ¬ Q is equivalent to P + Q.
Question 35.
Consider the following well-formed formulae:
I.¬∀x (P(x))
II. ¬∃x (P(x))
III.¬∃x (¬P(x))
IV. ∃x (¬P(x))
Which of the above are equivalent?
(a) I and III
(b) I and IV
(c) II and III
(d) II and IV
Answer/Explanation
Answer: (b) I and IV
Explanation:
I ¬∀xP(x) ≡ ∃x¬P(x)
and IV ∃x ¬P(x)
Clearly, choices I and IV are equivalent.
II ¬∃xP(x) ≡ ∀x ¬P(x)
and III ¬∃x[¬P(x)] ≡ ∀xP(x)
Clearly, II and III are not equivalent to each other or to I and IV.
![]()
Question 36.
Suppose the predicate F(x, y, t) is used to represent the statement that person x can fool person y at time t. Which one of the statements below expresses best the meaning of the formula ∀x∃y∃t (¬F(x, y, t))?
(a) Everyone can fool some person at some time
(b) No one can fool everyone all the time
(c) Everyone cannot fool some person all the time
(d) No one can fool some person at some time
Answer/Explanation
Answer: (b) No one can fool everyone all the time
Explanation:
∀x ∃y ∃t ¬ F(x, y, t)
≡ ¬{∃x ∀y ∀t F(x, y, t)}
≡ it is not true that (someone can fool all people at all times)
≡ no one can fool everyone all the time
Question 37.
Which one of the following options is CORRECT given three positive integers x, y, and z, and a predicate
P (x) = ¬ (x = 1) ∧ ∀y (∃z (x = y * z) ⇒ (y = x) ∨ (y = 1)
(a) P(x) being true means that x is a prime number
(b) P(x) being true means that x is a number other than 1
(c) P(x) is always true irrespective of the value of x
(d) P(x) being true means that x has exactly two factors other than 1 and x
Answer/Explanation
Answer: (a) P(x) being true means that x is a prime number
Explanation:
If P(x) is true, then
x ≠ 1 and also
x is broken into two factors, only if, one of the factors is x itself and the other factor is 1, which is exactly the definition of a prime number.
So P(x) is true means x is a prime number.
Question 38.
Consider the following logical inferences.
I1: If it rains then the cricket match will not be played.
The cricket match was played.
Inference: There was no rain.
I2: If it rains then the cricket match will not be played.
It did not rain.
Inference: The cricket match was played.
Which of the following is TRUE?
(a) Both I1 and I2 are correct inferences
(b) I1 is correct but I2 is not a correct inference
(c) I1 is not correct but I2 is a correct inference
(d) Both I1 and I2 are not correct inferences
Answer/Explanation
Answer: (b) I1 is correct but I2 is not a correct inference
Explanation:
Let p: It rains
q: cricket match will not be played.
I1: p ⇒ q
∴ \(\underline{\sim q}{\sim p}\)
Clearly I1 is correct since it is in the form of modus Tollens (rule of contrapositive)
I2: p ⇒ q
∴ \(\underline{\sim q}{\sim p}\)
which corresponds [p ⇒ q ∧~p] ⇒ ~ q
≡ [(p’ + q) p’] ⇒ q’
≡ [p’ + qp’] ⇒ q’
≡p’ ⇒ q’
≡(p’)’ + q’ ≡p + q’
which is not a tautology. So I2 is incorrect inference.
Question 39.
What is the correct translation of the following statement into mathematical logic?
“Some real numbers are rational”
(a) ∃x (real (x) ∨ rational (x))
(b) ∀x (real (x) → rational (x))
(c) ∃x (real (x) ∧ rational (x))
(d) ∃x (rational (x) → real (x))
Answer/Explanation
Answer: (c) ∃x (real (x) ∧ rational (x))
Explanation:
Some real numbers are rational ≡∃x [real (x) ∧rational (x)]
![]()
Question 40.
What is the logical translation of the following statements?
“None of my friends are perfect”
(a) ∃x (F(x) ∧ ¬ P(x))
(b) ∃x (¬ F(x) ∧ Fix))
(c) ∃x (¬ F(x) ∧ ¬P(x))
(d) ¬∃x (F(x) ∧ P(x))
Answer/Explanation
Answer: (d) ¬∃x (F(x) ∧ P(x))
Explanation:
None of my friends are perfect i.e., all of my friends are not perfect
∀x((F(x) → ¬ P(x))
∀x(¬ F(x) ∨¬ P(x))
¬ ∃x (F(x) ∧ P(x))
Alternatively
∃x (F(x) ∧ P(x)) gives
there exist some of my friends who are perfect, ¬∃x (F(x) ∧ P(x))
there does not exist any friend who is perfect i.e., none of my friends are perfect. So (d) is the correct option.
Question 41.
Which one of the following is NOT logically equivalent to ¬∃x(∀y(α) ∧ ∀z(β))
(a) ∀x(∃z(¬β) → ∀y(α))
(b) ∀x(∀z(β) → ∃y(¬ α))
(c) ∀x(∀y(α) → ∃z(¬β))
(d) ∀x(∃y(¬ α)∨ ∃z(¬β))
Answer/Explanation
Answer: (a) ∀x(∃z(¬β) → ∀y(α))
Explanation:
Let, ∀y(α) = p, ∀z(β) = Q
then, ∃y(¬α) = ¬p and ∃z (¬β) = ¬Q
Given, ¬∃x(∀y(α) ∧∀z(β))
= ¬∃x(P ∧ Q) = ¬∀x (¬P ∨¬Q)
= ∀x (P →¬Q)
(a) ∀x(∃z(¬β) → ∀y(α)) = ∀x (¬Q → P)
(b) ∀x(∀z(β) → ∃y(¬α)) = ∀x (Q → ¬ P)
= ∀x (P →¬Q)
(c) ∀x (∀x(α) → ∃z (¬β)) = ∀x (P → ¬ Q)
(d) ∀x (∃y(¬α) ∨ ∃z (¬β)) = ∀x (¬ P ∨ ¬ Q)
= ∀x (P → ¬ Q)
∴ Only (a) is not logocally equivalent to ∀x(P → ¬ Q).
Question 42.
Consider the statement:
“Not all that glitters is gold”
Predicate glitters(x) is true if x glitters and predicate gold(x) is true if x is gold. Which one of the following logical formulae represents the above statement?
(a) ∀x: glitters(x) ⇒ ¬gold(x)
(b) ∀x : gold(x) ⇒ glitters(x)
(c) ∃x : gold(x) ∧¬glitters(x)
(d) ∃x: glitters(x) ∧¬gold(x)
Answer/Explanation
Answer: (d) ∃x: glitters(x) ∧¬gold(x)
Explanation:
(a) ∀x glitters (x) ⇒¬gold (x) All glitters are not gold
(b) ∀x gold(x) ⇒ glitters(x) All golds are glitters
(c) ∃x gold(x) ∧ ¬ glitters(x) There exist gold which is not glitter i.e. not all golds are glitters.
(d) ∃x glitters(x) ∧ ¬ gold(x) Not all that glitters is gold i.e., there exist some which glitters and which is not gold.
Question 43.
Which one of the following propositional logic formulas is TRUE when exactly two of p, q, and r are TRUE?
(a) ((p ↔ q) ∧ r) ∨ (p ∧ q ∧ ~ r)
(b) (~ (p ↔ q) ∧ r) ∨ (p ∧ q ∧ ~ r)
(c) ((p → q) ∧ r) ∨ (p ∧ q ∧ ~ r)
(d) (~ (p ↔ q) ∧ r) ∧ (p ∧ q ∧ ~ r)
Answer/Explanation
Answer: (b) (~ (p ↔ q) ∧ r) ∨ (p ∧ q ∧ ~ r)
Explanation:
Option (b) is (~(p ↔ q) ∧ r) ∨ (p ∧ q ∧ ~r)
≡((p ⊕ q)r) + pqr’ ≡(pq’ + p’q)r + pqr’
≡pq’r + p’qr + pqr’ ≡pqr’ + pq’r + pq’r
This is exactly the mm-term form of a logical formula which is true when exactly two variables are true (only p, q true or only p, r true or the only q, r true).
Question 44.
Which one of the following Boolean expressions is NOT a tautology?
(a) ((a → b) ∧ (b → c)) → (a → c)
(b) (a ↔ c) → (~b → (a ∧ c))
(c) (a ∧ b ∧ c) → (c ∨ a)
(d) a →(b → a)
Answer/Explanation
Answer: (b) (a ↔ c) → (~b → (a ∧ c))
Explanation:
(a ↔ c) → (~ b → (a ∧c))
≡ (a ↔ c )’ + (b’ → ac)
≡(a ⊕ c)’ + (b’ → ac)
≡ac’ + a’c + b + ac
≡a(c’ + c) + a’c + b
≡a + a’c + b ≡a + c + b
which is not a tautology.
Question 45.
Consider the following statements:
P: Good mobile phones are not cheap
Q: Cheap mobile phones are not good
L: P implies Q
M: Q implies P
N: P is equivalent to Q
Which one of the following about L, M, and N is CORRECT?
(a) Only L is TRUE
(b) Only M is TRUE
(c) Only N is TRUE
(d) L, M, and N are TRUE.
Answer/Explanation
Answer: (d) L, M, and N are TRUE.
Explanation:
g: mobile is good
C: mobile is cheap
P: Good mobile phones are not cheap
g → c’ ≅ (g’ + c’)
Q: Cheap mobile phones are not good
c → g’ ≅ (c’ + g’)
:. Both P and Q are equivalent.
L: P → Q
M: Q → P
N: P ≡ Q
Since both P and Q are equivalent, all three of L. M, N are true. So the correct option is (d).
![]()
Question 46.
The CORRECT formula for the sentence, “not all rainy days are cold” is
(a) ∀d(Rainy (d)∧~Cold (d))
(b) ∀d (~Rainy (d) → Cold (d))
(c) ∃d (~Rainy (d) → Cold (d))
(d) ∃d (Rainy (d)∧ ~ Cold (d))
Answer/Explanation
Answer: (d) ∃d (Rainy (d)∧ ~ Cold (d))
Explanation:
Not (all rainy days are cold):
~ (∀d (Rainy (d) → Cold (d)))
≡~ (∀d (~ Rainy (d) ∨ Cold (d)))
≡ ∃d (Rainy (d)∧ ~ Cold (d))
Alternate Method:
Not all rainy days are cold is same as some rainy days are not cold which is the same as ∃d (Rainy (d)∧ ~ Cold (d))
Question 47.
Which one of the following is Not equivalent to p ↔ q?
(a) (¬p ∨ q) ∧ (p ∨¬ q)
(b) (¬p ∨ q) ∧ (q → p)
(c) (¬p ∧ q) ∨ (p ∧ ¬q)
(d) (¬p ∧¬q) ∨ (p ∧ q)
Answer/Explanation
Answer: (c) (¬p ∧ q) ∨ (p ∧ ¬q)
Explanation:
Here, option (a) and (b) can be reduced to (p → q) ∧ (q → p) and hence = p ↔ q
Option (d) is p’q’ + pq ≡ p ↔ q.
Option (c) is p’q + pq’ = p ⊕ q which is not equivalent to p ↔ q.
Question 48.
The binary operator ≠ is defined by the following truth table.
Table
Which one of the following is true about the binary operator ≠ ?
(a) Both commutative and associative
(b) Commutative but not associative
(c) Not commutative but associative
(d) Neither commutative nor associative
Answer/Explanation
Answer: (a) Both commutative and associative
Explanation:
The given truth table corresponds to p’q + pq’ = P ⊕ q. ⊕ is known to be both commutative and associative.
Question 49.
Consider the following two statements:
S1: If a candidate is known to be corrupt, then he will not be elected.
S2: If a candidate is kind, he will be elected. Which one of the following statements follows from S1 and S2 as per sound inference rules of logic?
(a) If a person is known to be corrupt, he is kind
(b) If a person is not known to be corrupt, he is not kind
(c) If a person is kind, he is not known to be corrupt
(d) If a person is not kind, he is not known to be corrupt
Answer/Explanation
Answer: (c) If a person is kind, he is not known to be corrupt
Explanation:
C: Person is corrupt
K: Person is kind.
E : Person is elected
S1 : C → \(\bar{E}\)
S2: K → E
S2 ↔ \(\bar{E}\) → \(\bar{K}\)
So from S1 and S2:(C → \(\bar{E}\)) ∧ (\(\bar{E}\) → \(\bar{K}\)) ≅ C → \(\bar{K}\) We can conclude C → \(\bar{K}\) which is same as K → \(\bar{C}\), which is same as option (c).
Question 50.
Which one of the following well-formed formulae is a tautology?
(a) ∀x ∃y R(x, y) ↔ ∃y ∀x R(x, y)
(b) (∀x [∃y R(x, y) → S(x, y)]) → ∀x ∃y S(x, y)
(c) [∀x ∃y (P(x, y) → R(x, y))] ↔ [∀x ∃y (¬P(x, y) ∨R(x, y))]
(d) ∀x ∀y P(x, y) → ∀x ∀y P(y, x)
Answer/Explanation
Answer: (c) [∀x ∃y (P(x, y) → R(x, y))] ↔ [∀x ∃y (¬P(x, y) ∨ R(x, y))]
Explanation:
Since P → R ≡¬P ∨R, and both the sides are the same (∀x∃y) Option (e) is clearly a tautology.
![]()
Question 51.
In a room, there are only two types of people, namely, Type 1 and Type 2. Type 1 people always tell the truth and Type 2 people always lie. You give a fair coin to a person in that room, without knowing which type he is from and tell him to toss it and hide the result from you till you ask for it. Upon asking, the person replies the following:
“The result of the toss is head if and only if I am telling the truth.”
Which of the following options is correct?
(a) The result is head
(b) The result is tail
(c) If the person is of Type 2, then the result is tail
(d) If the person is of Type 1, then the result is tail
Answer/Explanation
Answer: (a) The result is head
Explanation:
Type 1 always tells truth.
Type 2 always tells lies.
The statement is “toss is head if and only if I am telling the truth”.
There are two cases possible.
Case-1: Let the person be type 1.
Case-2: Let the person be type 2.
In each case, we shall prove that result is head.
Case-1: Let the person be type 1. Type 1 always tells truth.
So the statement “toss is head if and only if I am telling the truth” is true.
So toss head ⇔ telling truth. Since type 1 is telling truth so toss head is also true. So in case, 1 the result is that the toss is head.
Case-2: Let the person be type 2. Type 2 always tells lies.
So the statement “toss is head if and only if I am telling the truth” is false.
So toss head ⇔ telling truth is false. So toss head ⊕ telling truth. So toss head and telling truth to have opposite truth values. Now, since type 2 telling truth is false, so toss head has to have the opposite truth value which is true.
So toss head is true. So in case 2 also, the result is head.
So in both cases, we have proved that the result is head.
So option (a) is correct.
Question 52.
Let p, q, r, s represent the following propositions.
p : x∈ {8, 9, 10, 11, 12}
q : x is a composite number
r : x is a perfect square
s : x is a prime number
The integer x ≥ 2 which satisfies ¬((p ⇒ q) ∧ (¬r ∨ ¬is)) is ______.
Answer/Explanation
Explanation: We wish to make
¬ ((p ⇒ q) ∧ (¬r ∨ ¬s)) = 1
⇒ (p ⇒ q) ∧ (¬r ∨ ¬s) = 0
⇒ (p ⇒ q) = 0
or ¬r ∨ ¬s = 0
Now (1) is satisfies only when p 1 and q = 0.
Equation (2) ¬r ∨ ¬s = 0, iff r ∧ s = 1
i.e. r 1 and s= 1
i.e. x is a perfect square and x is a prime number. Which is not possible so condition (2) cannot be satisfied by any x. So condition (1) must be satisfies which is p = 1 and q = 0 i.e. x e {8, 9, 10, 11, 12,) and x is not a composite. Now the only value of x which satisfies this is x = 11. So correct answer is x = 11.
Question 53.
Consider the following expressions:
(i) False
(ii) Q
(iii) True
(iv) P ∨ Q
(v) ¬Q ∨ P
The number of expressions given above that is logically implied by P∧(P ⇒ Q) is ______.
Answer/Explanation
Solution:
p∧(p ⇒ q) = p(p’ + q) =pq
Take (i) false
pq ⇒ false ≡ pq ⇒ 0
≡ (pq)’ + 0
≡ p’ + q’ + 0
≡ not valid
Take (ii)
pq ⇒ q = (pq)’ + q
≡ (pq)’ + q
≡ p’ + 1 = 1
≡ valid
Take (iii)
pq ⇒ true ≡ pq ⇒ 1
≡ (pq)’ + 1 ≡ 1
≡ valid
Take (iv)
pq ⇒ p + q ≡ (pq)’ + p + q
≡ P’ + q’ + P + q
≡ 1 + 1
≡ 1
≡ valid
Take (v)
pq ⇒ q’ + p ≡ (pq)’ + q’ + p
≡ p’ + q’ + q’ + p
≡ 1
≡ valid
So the number of expressions that are logically implied by p ∧ (p ⇒ q) is 4.
Question 54.
Which one of the following well-formed formulae in predicate calculus is NOT valid?
(a) (∀x p(x) ⇒ ∀xq(x)) ⇒ (∃x¬p(x) ∨ ∀xq(x))
(b) (∃xp(x) ∨∃xg(x)) ⇒ ∃x(p(x) ∨q(x))
(c) ∃x (p(x) ∧ q(x)) ⇒ (∃x p(x) ∧ ∃xq(x))
(d) ∀x (p(x) ∨ q(x)) ⇒ (∀x p(x) ∨ ∀xq(x))
Answer/Explanation
Answer: (d) ∀x (p(x) ∨ q(x)) ⇒ (∀x p(x) ∨ ∀xq(x))
Explanation:
∀x is only one way distribution over “∨” so let us check (d)
(d) ∀x (p(x) ∨ q(x)) ⇒ (∀x p(x) ∨ ∀xq(x))
Let LHS be true, so we have,
P1 ∨ q1 (true)
p2 ∨ q2 (true)
p3 ∨ q3 (true)
.
.
.
Now take p1 is true, q1 is false and p2 is false, q2 is true.
Now LHS is true, but RHS, ∀x p(x) is false (since p2 is false) and ∀x q(x) is also false (since q1 is false)
So, LHS ≠ RHS.
![]()
Question 55.
Consider the first-order logic sentence F : ∀x(∃yR(x,y)). Assuming non-empty logical domains, which of the sentences below are implied by F?
I. ∃y(∃x R(x,y))
II. ∃y(∀x R(x,y))
III. ∀y(∃x R(x,y))
IV. ¬∃x(∀y ¬R(x,y))
(a) IV only
(b) I and IV only
(c) II only
(d) II and III only
Answer/Explanation
Answer: (b) I and IV only
Explanation:
I. ∀x ∃y R(x,y) →∃y (∃x R(x,y)) is true, since ∃y (∃x R(x,y))
II. ∀x ∃y R(x,y) →∃y (∀x R(x,y)) is false Since ∃y when it is outside is stronger than when it is inside.
III. ∀x ∃y R(x,y) → ∀y ∃x R(x,y) is false Since R(x, y) may not be symmetric in x and y.
IV. ∀x ∃y R(x,y) →¬ (∃x ∀y ¬R(x,y)) is true since ¬ (∃x ∀y ¬R(x,y)) ≡∀x ∃y R (x,y)
So, IV will reduce to ∀x ∃y R(x,y) → ∀x ∃y R(x,y) which is trivially true.
So the correct answer is I and IV only which is an option (b).
Question 56.
The statement (¬p) ⇒ (¬q) is logically equivalent to which of the statements below?
I. P ⇒ q
II. q ⇒ p
III. (¬q) ∨ p
IV. (¬p) ∨ q
(a) I only
(b) I and IV only
(c) II only
(d) II and III only
Answer/Explanation
Answer: (d) II and III only
Explanation:
Statement p’ ⇒ q’ ≡p + q’
I. p → q ≡p’ + q
II. q → p ≡ q’ + p
III. (¬q ∨ p) ≡ q’ + p.
IV. (¬p ∨ q) ≡p’ + q
So, clearly, the given statement is the same as II and III only.
Question 57.
Let p, q and r be propositions and the expression (p → q)→r be a contradiction. Then, the expression (r→p)→q is
(a) A tautology
(b) A contradiction
(c) Always TRUE when p is FALSE
(d) Always TRUE when q is TRUE
Answer/Explanation
Answer:
(d) Always TRUE when q is TRUE
Explanation:
(p → q) → r = 0
i.e., (p’ + q)’ + r = 0
i.e., pq’ + r = 0
This is possible only if pq’ = 0 and r = 0 Now, pq’ = 0 iff p = 0 or q’ = 0
So, final solution is r = 0 and (p = 0 or q’ = 0) Now let us see
(r → p) → q
≡(r’ + p)’ + q ≡ rp’ + q but we have previously shown that r – 0 So, rp’ = 0
So, (r → p) → q ≡ rp’ + q ≡ 0 + q ≡ q
So, the truth value of (r → p) → q is the same as that of q. So It is true whenever q is true.
So option (d) is correct.
Note: Since we have shown that (p 0 (or) q’ = 0) is true,
Option (c) is false because when p is false i.e.,
when p = 0, q is free to be O or 1.
Question 58.
Let p, q, r denote the statements “It is raining”, “It is cold”, and “It is pleasant”, respectively. Then the statement “It is not raining and it is pleasant, and it is not pleasant only if it is raining and it is cold” is represented by
(a) (¬ p ∧ r) ∧ (¬r → (p ∧ q))
(b) (¬ p ∧ r) ∧ ((p ∧ q) → ¬r)
(c) (¬ p ∧ r) ∨ ((p ∧ q) → ¬r)
(d) (¬ p ∧ r) ∨ (r → (P ∧ q))
Answer/Explanation
Answer:
(a) (¬ p ∧ r) ∧ (¬r → (p ∧ q))
Explanation:
p : “It is raining”,
q : “It is cold”, and
r : “It is pleasant”
So the correct representation of “It is not raining and it is pleasant, and it is not pleasant only if it is raining and it is cold” is
(¬p ∧ r) ∧ (¬r only if p ∧q)≡(¬p ∧ r) ∧ (¬r → (p ∧ q))
Question 59.
Consider the first order predicate formula φ:∀x[∀z z|x ⇒∃w (w >x) ∧(∀z z | w ⇒ (( w = z) ∨ (z = 1)))]
Here ‘a | b’ denotes that ‘a divides b’, where a and b are integers. Consider the following sets:
S1:{1, 2, 3, …, 100}
S2: Set of all positive integers
S3: Set of all integers
Which of the above sets satisfy φ?
(a) S1 and S3
(b) S2 and S3
(c) S1 S2 and S3
(d) S1 and S2
Answer/Explanation
Answer:
(b) S2 and S3
Explanation:
∀x[∀z|x ⇒ ((z = x) ∨ (z = 1)) ⇒ ∃w (w > x) ∧(∀z z | w ⇒((w = z) ∨(z = 1))) ]
The predicate φ simply says that if z is a prime number in the set then there exists another prime number in the set which is larger. Clearly, φ is true in S2 and S3 since in a set of all integers as well as all positive integers, there is a prime number greater than any given prime number.
However, in S1 : {1, 2, 3 100} φ is false since for prime number 97 ∈ S1 there exists no prime number in the set which is greater.
Question 60.
Which one of the following predicate formulae is NOT logically valid?
Note that W is a predicate formula without any free occurrence of x.
(a) ∃x(p(x) ∧ W) ≡ ∃x p (x) ∧ W
(b) ∀x(p(x) → W) ≡ ∀xp(x) → W
(c) ∃x(p(x) → W) ≡ ∀xp(x) → W
(d) ∀x(p(x) ∨ W) ≡ ∀x p(x) ∨ W
Answer/Explanation
Answer: (b) ∀x(p(x) → W) ≡ ∀xp(x) → W
Explanation:
∀x (p(x) → W) ⇒ (∀x p(x)) → W is true.
But (∀x p(x)) → W ⇒ ∀x (p(x) → W) is false. Since if LHS is true then (P1 ∧ P2 ∧ P3 … ∧Pn ) → W will be true and RHS will be false since P1 W, itself will be false since only P1 true cannot make W true (we need all the P1, P2 … Pn to be true to make W true)
So LHS ⇒ RHS is true and RHS ⇒ LHS is false so LHS ≠ RHS.
So option (b) is invalid.
Note that option (c) is true because by Boolean algebra,
LHS = ∃x (p(x) → W) ≡ ∃x (~p(x) ∨ W) ≡ ∃x (~p(x)) ∨ W
RHS = ∀x p(x) → W ≡ ~(∀x p(x)) ∨ W ≡ ∃x ~p(x) ∨ W
So LHS = RHS.
![]()
Question 61.
Let p and q be two propositions. Consider the following two formulae in propositional logic.
S1: (¬ p ∧ (p ∨ q)) → p
S2: q → ( ¬ p ∧ (p ∨ q))
Which one of the following choices is correct?
(a) Neither S1 nor S2 is a tautology.
(b) Both S1 and S2 are tautologies.
(c) S1 is a tautology but S2 is not a tautology.
(d) S1 is not a tautology S2 is a tautology.
Answer/Explanation
Answer: (c) S1 is a tautology but S2 is not a tautology.
Explanation:
S1: (¬p ∧(p ∨q)) →p
S2: q → (¬p ∧(p ∨q))
S1 : [p’ (p + q)] →p
≡(p’p + p’q) →q
≡p’q →q
≡(p’q)’ + q
≡p + q’ + q
≡p + 1
≡1 (tautology)
S2: q → (p’ (p + q))
≡ q → (p’p + p’q)
≡ q → p’q
≡ q’ + p’q
≡ (q’ + p’) (q’ + q)
≡q’ + p’ (contigency) (not a tautology) So, option (c) S1 is a tautology and S2 is not a tautology is correct.
Question 62.
Choose the correct choice(s) regarding the following propositional logic assertion S:
S : ((p ∧ Q) →R) → ( (P ∧Q) →(Q → R))
(a) S is a tautology.
(b) S is neither a tautology nor a contradiction.
(c) The antecedent of S is logically equivalent to the consequent of S.
(d) S is a contradiction.
Answer/Explanation
Answer: (a) S is a tautology.(c) The antecedent of S is logically equivalent to the consequent of S.
Explanation:
S : ((P ∧ Q) → R) → ((P ∧ Q) → (Q → R))
≡ (pq → r) → (pq → (q → r))
≡ [(pq)’ + r] [(pq)’ + (q’ + r)]
≡ [(pq)’ + r]’ + [(pq)’ + q’ + r]
≡ [pq . r’] + [p’ + q’ + q’ + r]
≡ pqr’ + p’ + q’ + r
≡ (p + P’)(qr’ + p’) + q’ + r
≡ qr’ + p’ + q’ + r
≡ (q + q’)(r’ + q’) + p’ + r
≡ r’+ q’ + p’ + r = r’ + r + q’ + p’
≡ 1+ q’ + p’ = 1 (Tautology)
So, S is a tautology.
So, option (a) is true.
Option (b) and (d) are false.
Option (c) antecedent of S is
pq → r ≡ (pq)’ + r
≡ p’ + q’ + r
The consequent of S is pq → (q → r)
≡ (pq)’ + q’ + r
≡ p’ + q’ + q’ + r
≡ p’ + q’ + r
So,Antecedent of S ≡ Consequent of S So, option (c) is also true.
