Combinatorics Questions with Answers for Computer Science
![]()
Question 1.
(a) Solve the recurrence equations:
T(n) = T(n – 1) + n
T(1) = 1
(b) What is the generating function G(z) for the sequence of Fibonacci numbers?
Answer/Explanation
Explanation:
(a) T(n) = T(n – 1) + n
T2 – Tn – 1 n
For Homogeneous solution:
Tn -Tn – 1 = 0
t- 1 = 0
t = 1
Therefore, homogenous solution is
Tn = C(1)n = C
For Particular solution:
Let particular solution be (d0 + d1n)n
⇒ (d0 + d1n)n – (d0 + d1n – 1))(n – 1) = n
⇒ d0n + d1n2 – d0n + d0 – d1(n – 1)2 = n
⇒ d0n + d1n2 – d0n + d0 – d1(n2– 2n + 1) = n
⇒ d0 + 2d1n – d1 = n
d0 – d1 = 0 and 2d1 = 1
⇒ d0 = d1 and d1 = \(\frac{1}{2}\)
∴ d0 = d1 = \(\frac{1}{2}\)
So particular solution is,
\(\left(\frac{1}{2}+\frac{1}{2} n\right)\) × n = \(\frac{n(n+1)}{2}\) = \(\frac{n^{2}+n}{2}\)
So complete solution is,
T(n) C +\(\frac{1}{2}\)n{n +1)
Given, T( 1) = 1
1 = C + \(\frac{1}{2}\) × 1 × (1 + 1)
1 = C+ 1
C= 0
Therefore complete solution of the recurrence relation is T(n) = \(\frac{n(n+1)}{2}\).
(b) The Fibonacci numbers are defined as a0 = 1, a1 = 1
ar = ar – 1 + ar – 2 r ≥ 2
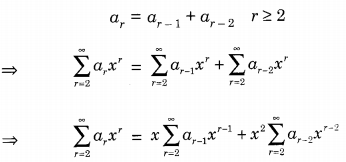
⇒ A(x) – a0 – a1 x = (A(x) – a0) + x2A(x)
Since, a0 = 1 and a1 = 1
⇒ A(x) – 1 – x = x(A(x) – 1) + x2A(x)
⇒ A(x) = \(\frac{1}{1-x-x^{2}}\)
Question 2.
Solve the recurrence equations:
T(n) = T\(\left(\frac{\mathrm{n}}{2}\right)\) + 1
T(1) = 1
Answer/Explanation
Explanation:
T(n) = T\(\left(\frac{\mathrm{n}}{2}\right)\) + 1
⇒ T(n) – T\(\left(\frac{\mathrm{n}}{2}\right)\) = 1
Let, n = 2k.
⇒ T(2k) – T\(\left(\frac{2^{\mathrm{k}}}{2}\right)\) = 1
⇒ T(2k) – T(2k – 1 = 1
Let, T(2k) – xk
xk – xk – 1 = 1
For Homogeneous solution:
xk – xk – 1 = 0
t – 1 = 0
t = 1
So homogeneous solution is: xk = C(1)k = C
For Particular solution:
Let particular solution be d1k
d1k – d1(k- 1) = 1
⇒ d1 = 1
Particular solution is k
∴ Complete solution is
xk = C + k
T(2k) = C + k
T(n) = C + log2n
Given, T(1) = 1
⇒ C= 1
∴ Complete solution is: T(n) = log2n + 1
Question 3.
How many substrings can be formed from a character string of length n?
Answer/Explanation
Explanation:
Let the string be of length 4 : abcd
Number of substrings of length 0=1 (only ε )
Number of substrings of length 1 = 4
a, b, c, d
Number of substrings of length 2 = 3
ab, bc, cd
Number of substrings of length 3 = 2
abc, bcd
Number of substrings of length 4=1
abcd
∴ Total number of substrings = 1 +(4+ 3 + 2 + 1)
= 1 + (Sum of 4 natural number)
= 1 + \(\frac{4 \times(4+1)}{2}\)
= 11
Therefore, total number of substrings (maximum) that can be formed from a character string of
length 1 + \(\frac{n(n+1)}{2}\).
![]()
Question 4.
The number of binary strings of n zeros and k ones that no two ones are adjacent is
(a) n+1CK
(b) nCK
(c) nCK+1
(d) None of these
Answer/Explanation
Answer: (a) n+1CK
Explanation:
First arranging all n zeros in a row. There is only 1 way for arranging n zeros in a row. By arranging n zeros in a row, we get (n + 1) positions to place ones.
So number of ways arranging k ones in (n + 1) positions = n + 1Ck
∴ Required number of binary strings of n zeroes and k ones that no two ones are adjacent = 1 × n + 1Ck = n + 1Ck.
Question 5.
The number of substrings (of all lengths inclusive) that can be formed from a character string of length n is
(a) n
(b) n2
(c) \(\frac{n(n-1)}{2}\)
(d) \(\frac{n(n+1)}{2}\)
Answer/Explanation
Answer: (d) \(\frac{n(n+1)}{2}\)
Explanation:
For a string of length n:
The number of substrings of length 1 = n
The number of substrings of length 2 = n – 1
The number of substrings of length 3 = n – 2 and so on…
The number of substrings of length n is 1 So total number of substrings ; = n + (n-1) + …+1
= Sum of n natural numbers.
= \(\frac{\mathrm{n}(\mathrm{n}+1)}{2}\)
Question 6.
In a room containing 28 people, there are 18 people who speak English, 15 people who speak Hindi and 22 people who speak Kannada. 9 persons speak both English and Hindi, 11 people speak both Hindi and Kannada whereas 13 persons speak both Kannada and English. How many people speak all three languages?
(a) 9
(b) 8
(c) 7
(d) 6
Answer/Explanation
Answer: (d) 6
Explanation:
E : Persons speaks English
H : Persons speaks Hindi
K : Persons speaks Kannada
Assume that everyone in the room speaks at least one of the languages.
Given, n(E ∪ H ∪ K) = 28
n(E) = 18
n(H) =15
n(K) = 22
n(E ∩ H) = 9
n(H ∩ K) = 11
n(K ∩ E) = 13
n(K ∩ E ∩ H) = ?
By principle of inclusion and exclusion
n(E ∪ H ∪ K) = n(E) + n(H) + n(K) – n(E ∩ H) – n(H ∩ E) – n(K ∩ E) + n(K ∩ E ∩ H)
28 = 18 + 15 + 22 – 9 – 11 – 13 + n(K ∩ E ∩ H) n(k ∩ E ∩ H) = 28 – 55 + 33 = 61 – 55 = 6
Therefore, the number of people who speak all three languages are 6.
![]()
Question 7.
Solve the following recurrence relation
xn = 2xn-1, n>1
x1 = 2
Answer/Explanation
Explanation:
xn = 2xn – 1 – 1
For Homogeneous solution:
xn = 2xn – 1 = 0
t – 2 = 0
t= 2
So homogeneous solution is
xn = C(2)n
For Particular solution:
Let particular solution be do.
d0 = 2d0 – 1
d0 = 1
So particular solution is 1
∴ Complete solution = Homogeneous solution + Particular solution
Complete solution = C(2)n + 1
⇒ xn = C(2)n + 1
Given initial condition is x1 = 2
2 = C(2)1 + 1
1 = 2C
C = \(\frac { 1 }{ 2 }\)
xn = \(\frac { 1 }{ 2 }\)(2)n + 1
∴ xn = 2n – 1 + 1
Question 8.
Two girls have picked 10 roses, 15 sunflowers and 14 daffodils. What is the number of ways they can divide the flowers among themselves?
(a) 1638
(b) 2100
(c) 2640
(d) None of these
Answer/Explanation
Answer: (c) 2640
Explanation:
Number of ways for distributing r similar things among n different things = (n – 1 + r)Cr
The number of ways for distributing 10 roses among the two girls = (2 – 1 + 10)C10 =11.
Similarly number of ways for distributing 15 sunflowers among two girls = (2 – 1 + 15)C15
= 16C15 = 16C1 = 16
Number of ways for distributing 14 daffodils among the two girls = (2 – 1 + 14)C14 = 15C14 = 15C1 =15
∴ Total number of ways = 11 × 16 × 15 = 2640
Question 9.
The minimum number of cards to be dealt from an arbitrarily shuffled deck of 52 cards to guarantee that three cards are from some same suit is
(a) 3
(b) 8
(c) 9
(d) 12
Answer/Explanation
Answer: (c) 9
Explanation:
Let the number of cards to be dealt from an arbitrarily shuffled deck of 52 cards be n.
Number of suits = 4
Required number of cards from the same suit = 3.
So by the pigeonhole principle
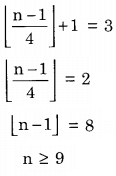
So the minimum number of cards to be dealt from an arbitrarily shuffled deck of 52 cards to guarantee that three cards are from the same suit is 9.
![]()
Question 10.
How many 4 digit even numbers have all 4 digits distinct?
(a) 2240
(b) 2296
(c) 2620
(d) 4536
Answer/Explanation
Answer: (b) 2296
Explanation:
The digits are given to be distinct i.e. no repetition. 4 digit even numbers cannot start with 0 and must end with 0, 2, 4, 6 or 8.
Since there is a condition for 0 in starting as well as ending we will count the even numbers ending with 0 separately.
So the total number of 4 digits even number = 4 digit even numbers ending with zero + 4 digit even numbers ending with 2, 4, 6, 8.
4 digit even numbers ending with 0
![]()
4 digit even numbers ending with 2, 4, 6, 8
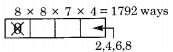
So the total number of 4 digit even numbers = 504+1792 = 2296.
Question 11.
The solution to the recurrence equation T(2k) = 3T(2k-1) + 1, T(1) = 1 is
(a) 2k
(b) \(\frac{\left(3^{\mathrm{k}+1}-1\right)}{2}\)
(c) 3log2k
(d) 2log3k
Answer/Explanation
Answer: (b) \(\frac{\left(3^{\mathrm{k}+1}-1\right)}{2}\)
Explanation:
T(2k) = 3T(2k – 1) + 1
Let, T(2k) = xn
⇒ xn = 3xn – 1 + 1
⇒ xn – 3xn – 1 = 1
So for Homogenous solution
xn – 3xn – 1 = 0
n – 3 = 0
n = 3
Homogenous solution is
xn = C1(3)n
T(2k) = C1(3)k
For Particular solution
Let d be the particular solution
d – 3d = 1
2d = -1
d = \(-\frac{1}{2}\)
Therefore, the complete solution is
T(2k) = C1(3)k \(-\frac{1}{2}\)
Given T(1) = 1
1 = C1(3)0 \(-\frac{1}{2}\)
1 = C1 \(-\frac{1}{2}\)
C1 = \(\frac { 3 }{ 2 }\)
So the complete solution is
T(2k) = C1 (3)k \(-\frac{1}{2}\)
Given, T(1) = 1
1 = C1(3)0 \(-\frac{1}{2}\)
1 = C1 \(-\frac{1}{2}\)
C1 = \(\frac { 3 }{ 2 }\)
So the complete solution is
T(2k) = \(\frac { 3 }{ 2 }\)(3)k \(-\frac{1}{2}\)
T(2k) = \(\frac{3^{\mathrm{k}+1}-1}{2}\)
Question 12.
The minimum number of colors required to color the vertices of a cycle with n nodes in such a way that no two adjacent nodes have the same color is
(a) 2
(b) 3
(c) 4
(d) n – 2\(\left[\frac{n}{2}\right\rfloor\)+2
Answer/Explanation
Answer: (d) n – 2\(\left[\frac{n}{2}\right\rfloor\)+2
Explanation:
The minimum number of colors required to color the vertices of a cycle with n nodes = 2, when n is even = 3, when n is odd
Therefore n – 2 \(\left\lfloor\frac{\mathrm{n}}{2}\right\rfloor\) +2 gives 2 when n is even. and 3 when n is odd.
![]()
Question 13.
Let A be a sequence of 8 distinct integers sorted in ascending order. How many distinct pairs of sequences, B and C are there such that (i) each are sorted in ascending order, (ii) B has 5 and C has 3 elements, and (iii) the result of merging B and C gives A?
(a) 2
(b) 30
(c) 56
(d) 256
Answer/Explanation
Answer: (c) 56
Explanation:
This corresponds to an ordered partition of 8 elements into two groups, the first with 5 elements and second with 3 elements. The number of ways of doing this is p(8; 5, 3) = \(\frac{8 !}{5 ! 3 !}\) = 56
Question 14.
n couples are invited to a party with the condition that every husband should be accompanied by his wife. However, a wife need not be accompanied by her husband. The number of different gatherings possible at the party is
(a) \(\left(\begin{array}{c}
2 n \\
n
\end{array}\right)\) * 2n
(b) 3n
(c) \(\frac{(2 n) !}{2^{n}}\)
(d) \(\left(\begin{array}{c}
2 n \\
n
\end{array}\right)\)
Answer/Explanation
Answer: (b) 3n
Explanation:
For each of the n couples invited to the party one of three things is possible:
1. Both husband and wife attend the party.
2. Wife only attends the party.
3. Neither husband nor wife attends the party. Since there are n such couples, a total number of possibilities = 3n.
Question 15.
Mala has a colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour-pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?
(a) 9
(b) 8
(c) 7
(d) 6
Answer/Explanation
Answer: (d) 6
Explanation:
The problem reduces to finding how many distinct ordered color pairs (C1, C2) are possible with k colors.
Since the first color C1 can be any one of the k colors and the second color C2 also can be any one of the k colors (both prints of a letter can be colored with the same color), the total no. of such order color pairs is equal to k × k = k2.
Since each pair of letters must be colored with different color pairs, at least 26 color pairs are required to do this.
Therefore the requirement is k2 ≥ 26.
The minimum value of k that satisfies this equation is k = 6.
![]()
Question 16.
In how many ways can we distribute 5 distinct balls, B1, B2……., B5 in 5 distinct cells, C1 C2, …, C5 such that Ball Bi is not in cell Ci,∀i = 1,2,…,5 and each cell contains exactly one ball?
(a) 44
(b) 96
(c) 120
(d) 3125
Answer/Explanation
Answer: (a) 44
Explanation:
We want every one of the 5 balls to be in the wrong box. This is nothing but the number of derangements of a set of 5 elements = D5. i.e. we need to compute D5
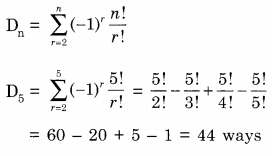
Question 17.
Let n = p2q, where p and q are distinct prime numbers. How many numbers m satisfy 1 ≤ m ≤ n and gcd (m, n) = 1? Note that gcd (m, n) is the greatest common divisor of m and n.
(a) p(q – 1)
(b) pq
(c) (p2 – 1)(q – 1)
(d) p(p – 1)(q – 1)
Answer/Explanation
Answer: (d) p(p – 1)(q – 1)
Explanation:
The number of numbers from 1 to n, which are relatively prime to n i.e., gcd (m, n) = 1, is given by the Euler Totient function Φ(n). If n is broken down into its prime factors as n = p1n1 . p2n2 ……
where p1,p2 etc. are distinct prime numbers, then
Φ(n) = Φ( p1n1) Φ(p2n2)
Here, n = p2 q
So, Φ(n) = Φ(p2) × Φ(q)
Now, using the property Φ(pk) = pk – pk – 1
Φ(p2) = p2 – p1 = p2 – p and
Φ(q) = q1 – q0 = q – 1
Substituting these in eq. (i), we get
Φ(n) = (p2 – p) (q – 1)
= p(p – 1) (q – 1)
Question 18.
What is the minimum number of ordered pairs of non-negative numbers that should be chosen to ensure that there are two pairs (a, b) and (c, d) in the chosen set such that a=c mod 3 and b = d mod 5
(a) 4
(b) 6
(c) 16
(d) 24
Answer/Explanation
Answer: (c) 16
Explanation:
The number of combinations of pairs (a mod 3, b mod 5) is 3 × 5 = 15 (since a mod 3 can be 0, 1, or 2) and b mod 5 can be 0, 1, 2, 3 or 4)
∴ If 16 different ordered pairs are chosen at least 2 of them must have (a mod 3, b mod 5) as same (basic pigeon hole principle).
Let such two pairs be (a, b) and (c, d) then
a mod 3 ≡ c mod 3 ⇒ a ≡ c mod 3, and b mod 5 ≡ d mod 5 ⇒ b ≡ d mod 5
Question 19.
Let G(x) = 1/(1 – x)2 = \(\sum_{x=1}^{∞}\)g(i)xi where |x| < 1. what is g(i)?
(a) i
(b) i + 1
(c) 2i
(d) 2i
Answer/Explanation
Answer: (b) i + 1
Explanation:

![]()
Question 20.
For each element in a set of size 2n, an unbiased coin is tossed. The 2n coin tossed are independent. An element is chosen if the corresponding coin toss were head. The probability that exactly n elements are chosen is
(a) \(\left(\begin{array}{c}
2 n \\
\mathrm{n}
\end{array}\right) / 4^{\mathrm{n}}\)
(b) \(\left(\begin{array}{c}
2 n \\
n
\end{array}\right) / 2^{n}\)
(c) \(1 /\left(\begin{array}{c}
2 \mathrm{n} \\
\mathrm{n}
\end{array}\right)\)
(d) \(\frac { 1 }{ 2 }\)
Common Data for Q.21 & Q.22
Suppose that a robot is placed on the Cartesian plane. At each step it is allowed to move either one unit up or one unit right, i.e., if it is at (i, j) then it can move to either (i + 1, j) or (i, j + 1).
Answer/Explanation
Answer:
(a) \(\left(\begin{array}{c}
2 n \\
\mathrm{n}
\end{array}\right) / 4^{\mathrm{n}}\)
Explanation:
The probability that exactly n elements are chosen = The probability of getting n heads out of 2n tosses
= 2nCn (1/2)n (1/2)2n – n(Binomial formula)
= 2nCn (1/2)n (1/2)n
= \(\frac{{ }^{2 \mathrm{n}} \mathrm{C}_{\mathrm{n}}}{2^{2 \mathrm{n}}}\) = \(\frac{{ }^{2 n} \mathrm{C}_{\mathrm{n}}}{\left(2^{2}\right)^{\mathrm{n}}}\) = \(\frac{{ }^{2 \mathrm{n}} \mathrm{C}_{\mathrm{n}}}{4^{\mathrm{n}}}\)
Question 21.
How many distinct paths are there for the robot to reach the point (10,10) starting from the initial position (0, 0)?
(a) \(\left(\begin{array}{l}
20 \\
10
\end{array}\right)\)
(b)220
(c)210
(d) None of these
Answer/Explanation
Answer:
(a) \(\left(\begin{array}{l}
20 \\
10
\end{array}\right)\)
Explanation:
Consider the following diagram:
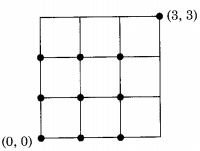
The robot can move only right or up as defined in the problem. Let us denote the right move by ‘R’ and the up move by ‘U’. Now to reach (3, 3) from (0, 0), the robot has to make exactly 3 ‘R’ moves and 3 ‘U’ moves in any order. Similarly to reach (10, 10) from (0, 0), the robot has to make 10 ‘R’ moves and 10 ‘U’ moves in any order. The number of ways this can be done is the same as the number of permutations of a word consisting of 10 ‘R’s and 10 ‘U’s.
Applying formula of permutation with limited repetitions we get the answer as \(\frac{20 !}{10 ! 10 !}\) = 20C10.
Question 22.
Suppose that the robot is not allowed to traverse the line segment from (4, 4) to (5, 4). With this constraint, how many distinct paths are there for the robot to reach (10,10) starting from (0,0)?
(a) 29
(b) 219
(c) \(\left(\begin{array}{l}
8 \\
4
\end{array}\right) \times\left(\begin{array}{c}
11 \\
5
\end{array}\right)\)
(d) \(\left(\begin{array}{l}
20 \\
10
\end{array}\right)-\left(\begin{array}{l}
8 \\
4
\end{array}\right) \times\left(\begin{array}{c}
11 \\
5
\end{array}\right)\)
Answer/Explanation
Answer:
Explanation:
The robot can reach (4, 4) from (0,0) in 8C4 ways as argued in the previous problem. Now after reaching (4,4), the robot is not allowed to go to (5,4). Let us count how many paths are there from (0,0) to (10, 10) if the robot goes from (4, 4) to (5, 4) and then we can subtract this from a total number of ways to get the answer.
Now there are 8C4 ways for robot to reach (4, 4) from (0, 0) and then robot takes the ‘U’ move from (4, 4) to (5, 4). Now from (5, 4) to (10, 10) the robot has to make 5 ‘U’ moves and 6 ‘R’ moves
in any order which can be done in \(\frac{11 !}{5 ! 6 !}\) ways = 11C5 ways.
∴ The number of ways robot can move from (0,0) (10, 10) via (4, 4) – (5, 4) move is
8C4 × 11C5 = \(\left(\begin{array}{l}
8 \\
4
\end{array}\right)\) × \(\left(\begin{array}{c}
11 \\
5
\end{array}\right)\)
∴ Number of ways robot can move from (0,0) to (10, 10) without using (4, 4) to (5, 4) move is
\(\left(\begin{array}{l}
20 \\
10
\end{array}\right)\) – \(\left(\begin{array}{l}
8 \\
4
\end{array}\right)\) x \(\left(\begin{array}{l}
11 \\
5
\end{array}\right)\) ways.
Which is an option (d).
![]()
Question 23.
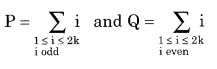
where k is positive integer. Then
(a)P = Q – k
(b)P=Q + k
(c) P = Q
(d) P = Q + 2k
Answer/Explanation
Answer:
Common Data for Q.24 & Q.25
Let xn denote the number of binary strings of length n that contain no consecutive 0s.
Explanation:
P = Σ i = 1 + 3 + 5 + 7 + … + (2k – 1)
1 ≤ i ≤ 2k, i is odd
Q= Σ i=2+4+ 6+…2k, 1 < i < 2k, 1 ≤ i ≤ 2k, i is even.
P is in A.P with a = 1, d = 2 and n = k
Q is in A.P with a = 2, d = 2 and n = k
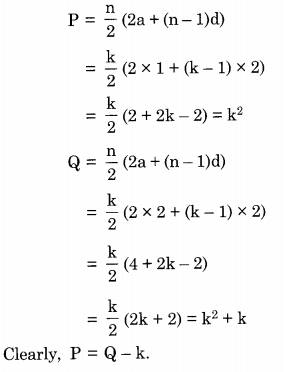
Question 24.
Which of the following recurrences does xn satisfy?
(a) xn = 2xn – 1
(b) xn = x[n/2] + 1
(c) xn = x[n/2] + n
(d) xn = xn – 1 + xn – 2
Answer/Explanation
Answer: (d) xn = xn – 1 + xn – 2
Explanation:
The ✓ represents those strings with no consecutive 0’s.
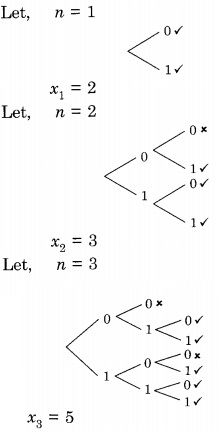
Now, substituting n = 3 in all of the answers only choice (d) xn = xn – 1 + xn – 2 satisfies the numbers obtained from the tree counting.
Question 25.
The value of x5 is
(a) 5
(b) 7
(c) 8
(d) 13
Answer/Explanation
Answer: (d) 13
Explanation:
x1 = 2
x2 = 3
⇒ x3 = x1 + x2 = 2 + 3 = 5
⇒ x4 = 2 + x3 = 3 + 5 = 8
⇒ x5 = 3 + x4 = 5 + 8 = 13
So option (d) is correct.
Question 26.
The exponent of 11 in the prime factorization of 300! is
(a) 27
(b) 28
(c) 29
(d) 30
Answer/Explanation
Answer: (c) 29
Explanation:
In 300!, distinct numbers divisible by 11 = \(\left[\frac{300}{11}\right\rfloor\) = 27.
Since these 27 numbers contain, the same number which can be further divisible by 11 i.e.
\(\left[\frac{27}{11}\right\rfloor\) = 2(121 and 242)
So, total number of 11’s = 27 + 2 = 29 Hence exponent of 11 is 29.
Question 27.
In how many ways can b blue balls and r red balls be distributed in re distinct boxes?
(a) \(\frac{(n+b-1) !(n+r-1) !}{(n-1) ! b !(n-1) ! r !}\)
(b) \(\frac{(n+(b+r)-1) !}{(n-1) !(n-1) !(b+r) !}\)
(c) \(\frac{n !}{b ! r !}\)
(d) (n + (b + r) -1)! /n!(b + r – 1)
Answer/Explanation
Answer: (a) \(\frac{(n+b-1) !(n+r-1) !}{(n-1) ! b !(n-1) ! r !}\)
Explanation:
A number of ways to distribute ‘b’ blue balls in n distinct boxes:
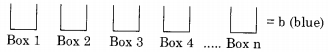
Since each box can contain 0 to n blue balls, so number of ways
= ( n + b – 1)C(n – 1)
=\(\frac{(n+b-1) !}{(n-1) ! \times b !}\)
Number of ways to distribute ‘r’ red balls in n distinct boxes:
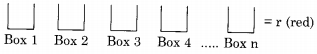
Since each box can contain 0 to n red balls. So number of ways = ( n + r – 1)C(n – 1)
=\(\frac{(n+r-1) !}{(n-1) ! \times r !}\)
Since both are independent of each other So total ways = Number of ways to distribute ‘b’ blue balls x Number of ways to distribute ‘r’ red balls
= \(\frac{(n+b-1) !(n+r-1) !}{(n-1) ! \times b !(n-1) ! \times r !}\)
![]()
Question 28.
A pennant is a sequence of numbers, each number being 1 or 2. An n-pennant is a sequence of numbers with a sum equal to n. For example, (1,1,2) is a 4-pennants. The set of all possible 1-pennant is {(1)}, the set of all possible 2-pennants is {(2), (1,1)}and the set of all 3-pennants is {(2,1), (1,1,1), (1,2)}. Note that the pennant (1,2) is not the same as the pennant (2,1). The number of 10-pennants is ______.
Answer/Explanation
Explanation:
In a 10-pennant let there we x1 ones and x2 twos. So we need to find all the solutions of
x1 + 2x2 = 10
put, x1 = 0 ⇒ x2 = \(\frac { 10 }{ 2 }\) = 5
So, (0, 5) is a solution i.e. a 10-pennant could have 0 ones and 5 twos. The number of ordered permutations of 0 ones and 5 twos = 5!/ 5! = 1
Now x1 cannot be 1 since in that case x2 = \(\frac { 10 }{ 2 }\) = 4.5
(is not an integer).
put, x1 = 2 ⇒ x2 = \(\frac { 8 }{ 2 }\) = 4
So, (2, 4) is a solution i.e. a 10-pennant could have 2 ones and 4 twos. The number of ordered permutations of 2 ones and 4 twos
\(\frac{6 !}{2 ! 4 !}\) = 15
Similarly (4, 3), (6, 2), (8, 1) and (10,0) are the other four solutions and the number of pennants for each is respectively
\(\frac{7 !}{4 ! 3 !}\) = 35, \(\frac{8 !}{6 ! 2 !}\) =28, \(\frac{9 !}{8 ! 1 !}\) = 9, \(\frac{10 !}{10 ! 10 !}\) = 1 = 89
So the total number of 10-pennants = 1 + 15 + 35 + 28 + 9 + 1 = 89
Question 29.
Each of the nine words in the sentence
“The quick brown fox jumps over the lazy dog”
is written on a separate piece of paper. These nine pieces of paper are kept in a box. One of the pieces is drawn at random from the box. The expected length of the word drawn is _____. (The answer should be rounded to one decimal place).
Answer/Explanation
Explanation:
“The quick brown fox jumps over the lazy dog” (3) (5) (5) (3) (5) (4) (3) (4) (3)
Now let x be the number of letters in the word that is randomly picked.
Now, we make a probability distribution table for x

From this table we can easily find the expected value of x.
E(x) = Σx p(x)
= 3 × \(\frac { 4 }{ 9 }\) + 4 × \(\frac { 2 }{ 9 }\) + 5 × \(\frac { 3 }{ 9 }\) = \(\frac { 35 }{ 9 }\) = 3.88 = 3.9
(after rounding to one decimal accuracy).
Question 30.
The number of distinct positive integral factors of 2014 is _______.
Answer/Explanation
Explanation:
Factorizing 2014 in primes by successively dividing by primes, we get
2014 = 21 × 191 × 531
Now We use the formula:
If n = p1n1 . p2n2…..prnr is the prime factorization of n, then the number of distit factors of n is given by (n1 + 1) × (n2 + 1) …….. (nr + 1).
Now since 2014 = 21 × 191 × 531, the number of distinct factors of 2014 = (1 + 1) (1 + 1) (1 + 1) = 2 × 2 × 2 = 8
Question 31.
\(\sum_{x=1}^{99} \frac{1}{x(x+1)}\) = _______.
Answer/Explanation
Explanation:
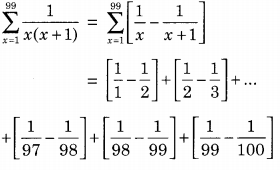
= 1 – \(\frac { 1 }{ 100 }\) (all the terms in above series except the first and last terms cancels out)
= \(\frac { 99 }{ 100 }\) = 0.99
![]()
Question 32.
Let an represent the number of bit strings of length n containing two consecutive 1s. What is the recurrence relation for an?
(a) an -2 + an – 1 + 2n – 2
(b) an -2 + 2an – 1 + 2n – 2
(c) 2an -2 + an – 1 + 2n – 2
(d) 2an -2 + 2an – 1 + 2n – 2
Answer/Explanation
Answer: (a) an -2 + an – 1 + 2n – 2
Explanation:
a1 = 0 [n0 strings of length 1 contain two consecutive 1’s]
a2 = 1 [∴ strings = 11]
a3 = 3 [∴ strings are : 011, 110, 111]
a4 = 8 [∴ strings are : 0011, 0110, 0111, 1011, 1100, 1101, 1110, 1111]
Option (a):
an = an – 2 + an – 1 + 2n – 2
⇒ a4 = a4 – 2 + a4 – 1 + 24 – 2
= a2 + a3 + 22
= 1 + 3 + 4 = 8 which is true.
Option (b):
an = an – 2 + 2an – 1 + 2n – 2
⇒ a4 = a2 + 2a3 + 22
= 1 + 2 × 3 + 4 = 11 which is False.
Option (c):
an = 2an – 2 + an – 1 + 2n – 2
⇒ a4 = 2a2 + a3 + 22
= 2 × 1 + 3 + 4 = 9 which is false.
Option (d):
an = 2an – 2 + 2an – 1 + 2n – 2
⇒ a4 = 2a2 + 2a3 + 22
= 2 × 1 + 2 × 3 + 4 = 12 which is false.
∴ Option (a) : an = an – 2 + an – 1 + 2n – 2 is correct.
Question 33.
The number of divisors of 2100 is _______.
Answer/Explanation
Explanation:
Dividing 2100 successively by prime numbers, we get that, the prime factors of 2100 are 2 × 2 × 3 × 5 × 5 × 7
⇒ 22 × 31 × 52 × 71
If N = pk1 × qk2 × rk3…… × ykn
then the number of factors of N are (k1+1) (k2+1) … (kn+1)
∴ For 2100 we have (2 + 1) (1 + 1) (2 + 1) (1 + 1) = 36 factors.
Question 34 .
The number of 4 digit numbers having their digits in non-decreasing order (from left to right) constructed by using the digits belonging to the set {1, 2, 3} is ____.
Answer/Explanation
Explanation:
To satisfy the non-decreasing order condition allow 1, 2, 3 after 1, allow only 2, 3 after 2 and allow only 3 after 3. The following tree diagram gives all the allowed numbers satisfying the given condition.
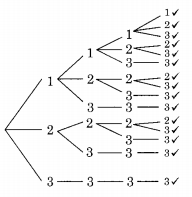
All the tick-marked numbers satisfy the non-decreasing order condition.
⇒ A number of 4-digit numbers = Number of tick marks = 15.
Question 35.
Let an be the number of re-bit strings that do NOT contain two consecutive l’s. Which one of the following is the recurrence relation for an?
(a) an = an – 1 + 2an – 2
(b) an = an – 1 + an – 2
(c) an = 2an – 1 + an – 2
(d) an = 2an – 1 + 2an – 2
Answer/Explanation
Answer: (d) an = 2an – 1 + 2an – 2
Explanation:
Let an be the number of n-bit strings that do not contain two consecutive 1’s. we wish to develop a recurrence relation for an.
Consider 1 bit strings 0, 1 So, a1 = 2
Consider 2 bit strings 00, 01, 10, 11
Out of minimum only 00, 01, 10 do not contain two consecutive 1’s.
So, a2 = 3

Out of minimum six strings only 000, 001, 010, 100 and 101 five strings satisfy do not contain two consecutive 1’s. So, a3 = 5. Three numbers a1, a2, a3 satisfy clearly only (b) an = an – 1 + an – 2 is correct.
Question 36.
The coefficient of x12 in (x3 + x4 + x5 + x6 +…)3 is _______.
Answer/Explanation
Explanation:
We wish to find coefficient of x12 in (x3 + x4 + x5 +…)3
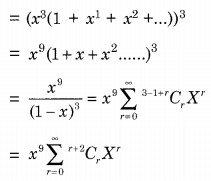
Now to make x12 we need to put r = 3 So coefficient of x12 is 3 + 2C3 = 5C3 = 5C2 = 10
Question 37.
Consider the recurrence relation a1 = 8, an = 6n2 + 2n + an – 1 Let a99 = K × 104. The value of K is ______.
Answer/Explanation
Explanation:
Given, an = 6n2 + 2 n + an – 1 and a1 = 8
We wish to find a99
Now,
a2 = 6 × 22 + 2 × 2 + a1
a3 = 6 × 32 + 2 × 3 + a2
= 6 × 32 + 2 × 3 + 6 × 22 + 2 × 2 + a1………
a99 = 6 × 992 + 2 × 99 + 6 × 982 + 2 + 98 ….
…. + 6 × 22 + 2 × 2 + a1
Since,
a1 = 8
a99 = 6 × 992 + 2 × 99 + 6 × 982 + 2 × 98…….
……+ 6 × 22 + 2 × 2 + 8
= 6 × 992 + 2 × 99 + 6 × 982 + 2 × 98…
…6 × 22 + 2 × 2 + 6 × 12 + 2 × 1
= 6(12+22+32… 992)+ 2.(1 + 2 + 3…99)
= 6. \(\frac{(99(99+1)(2 \times 99+1))}{6}\) + 2 \(\left(\frac{99(99+1)}{2}\right)\)
= 99 × 100 × 199 + 99 × 100
= 100 × 99 (199 + 1) = 100 × 99 × 200
= 2 × 99 × 104 = 198 × 104
So if a99 = K × 104 then K = 198.
Question 38.
If the ordinary generating function of a sequence \(\left\{a_{n}\right\}_{n=0}^{\infty} \text { is } \frac{1+z}{(1-z)^{3}}\) , then a3 – a0 is equal to _______.
Answer/Explanation
Explanation:
Given that generating function:
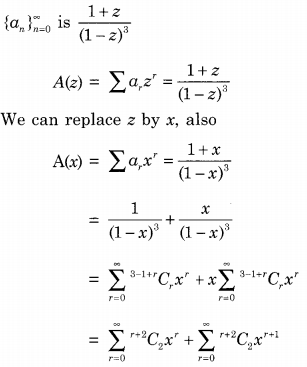
Now we read to find a0 and 3 which are nothing but the coefficient of x0 and x3 respectively.
a0 = coefficient x0 = (0 + 2)C2 = 2C2 = 1
a3 = coefficient x3 = (3 + 2)C2 = (2 + 2)C2
= 5C2 + 4C2 = 16
So, a3 – a0 = 16 – 1 = 15
![]()
Question 39.
Which one of the following is a closed form expression for the generating function of the sequence {a1n}, where an = 2n + 3 for all n = 0 1,2,…..?
(a) \(\frac{3}{(1-x)^{2}}\)
(b) \(\frac{3 x}{(1-x)^{2}}\)
(c) \(\frac{2-x}{(1-x)^{2}}\)
(d) \(\frac{3-x}{(1-x)^{2}}\)
Answer/Explanation
Answer: (d) \(\frac{3-x}{(1-x)^{2}}\)
Explanation:
Given, an = 2n + 3
Since generating function for 1 is \(\frac{1}{1-x}\) and n is \(\frac{x}{(1-x)^{2}}\), the generating function for an is
A(x) = \(\frac{2 x}{(1-x)^{2}}\) + \(\frac{3}{1-x}\)
= \(\frac{2 x+3(1-x)}{(1-x)^{2}}\) = \(\frac{3-x}{(1-x)^{2}}\)
which is option (d).
Question 40.
Let U = {1,2, ….., n} and A = {(x , X), x ∈ X and X ⊆ U}. Consider the following two statements om |A|.
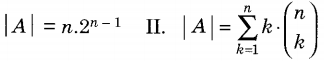
Which of the following is correct?
(a) Both I and II
(b) Neither I nor II
(c) Only II
(d) Only I
Answer/Explanation
Answer: (a) Both I and II
Explanation:
A – {(x, X), x ∈ X and X ⊆ U}
The number of k element subsets of a set U with n elements = \(\begin{aligned}
&n \\
&k
\end{aligned}\) = nCk
The number of possible ordered pairs (x, X) where x ∈ X is k. nCk for a given value of k from 1 to n.
So total number of ordered pairs in A
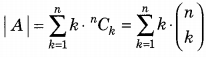
So II is correct, (Note that k = 0 is excluded since the empty set has no elements and cannot form an ordered pair such as (x, X)).
But since by the combinational identity
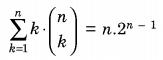
So I am also correct.
So both I and II are correct.
Question 41.
The number of permutations of the characters in LILAC so that no character appears in its original position, if the two L’s are indistinguishable, is_________.
Answer/Explanation
Explanation:
Since both L’s are indistinguishable.
First L’s can be arranged in 3 positions 2, 3, or 5 in 3C2 = 3 ways as follows:
_ L _ L _
or _ L _ _ L
or _ _ _ L L
Now the letters I, A, C can be deranged in 2 x 2! ways. Example in _ L _ L _. C cannot occupy 5th position, so only 2 ways.
The remaining I and A can be arranged in the remaining 2 positions in 2! ways = 2 ways.
So answer is 3 × 2 × 2! = 12.
Question 42.
There are 6 jobs with distinct difficulty levels, and 3 computers with distinct processing speeds. Each job is assigned to a computer such that:
• The fastest computer gets the toughest job and the slowest computer gets the easiest job.
• Every computer gets at least one job.
The number of ways in which this can be done is ______.
Answer/Explanation
Explanation:
Let computers be A, B, and C
The toughest job assigned to the fastest computer (Say, A) is 1 way.
The easiest job assigned to the shortest computer (Say, B) is 1 way.
The remaining 4 jobs are to be assigned to 3 computers so that computer C gets at least one job since A and B have already been assigned a job.
A number of ways 4 jobs assigned to 3 computers = 34.
The number of ways 4 jobs assigned to 3 computers so that computer C does not get any job = 24. Required number of ways = 34 – 24 = 81 – 16 = 65 ways
