- Write a C program to print lower triangular matrix of a square matrix
The main diagonal of a square matrix divides it into two sections, one above the diagonal and the other one is below the diagonal. If all elements in lower-section consists of zeros, it is a upper-triangular matrix and If all elements in upper-block consists of zeros, it is a lower-triangular matrix.
A lower triangular matrix is a square matrix in which all the elements above the main diagonal are zero. The variable L is commonly used to represent a lower triangular matrix.
Example of Lower Triangular Matrix: 1 0 0 0 2 3 0 0 4 5 6 0 7 8 9 1
Points to remember
Let A be the input matrix and L be the lower triangular matrix of A.
- All the elements above major diagonal of L are zero.
L[i][j] = 0, If i < j. - L[i,j] = A[i,j], If i >= j.
- A matrix is upper and lower triangular both if and only if it is a diagonal matrix.
C program to print lower triangular matrix
This program, takes a square matrix as input from user and then prints the lower triangular matrix of input matrix. It traverse the input matrix row wise(first all elements of a row from left to right, then jump to next row) using two loops(check line number 27 and 28 of below program). For every element, it compares whether row index is less than column index. If row index is less than column index then it prints zero other wise prints the current element on screen.
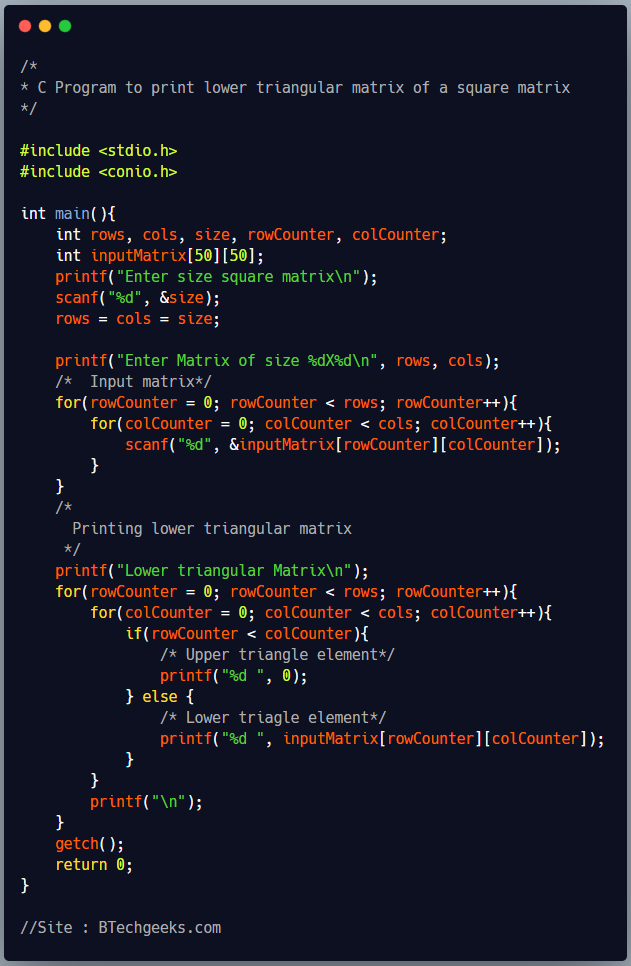
/*
* C Program to print lower triangular matrix of a square matrix
*/
#include <stdio.h>
#include <conio.h>
int main(){
int rows, cols, size, rowCounter, colCounter;
int inputMatrix[50][50];
printf("Enter size square matrix\n");
scanf("%d", &size);
rows = cols = size;
printf("Enter Matrix of size %dX%d\n", rows, cols);
/* Input matrix*/
for(rowCounter = 0; rowCounter < rows; rowCounter++){
for(colCounter = 0; colCounter < cols; colCounter++){
scanf("%d", &inputMatrix[rowCounter][colCounter]);
}
}
/*
Printing lower triangular matrix
*/
printf("Lower triangular Matrix\n");
for(rowCounter = 0; rowCounter < rows; rowCounter++){
for(colCounter = 0; colCounter < cols; colCounter++){
if(rowCounter < colCounter){
/* Upper triangle element*/
printf("%d ", 0);
} else {
/* Lower triagle element*/
printf("%d ", inputMatrix[rowCounter][colCounter]);
}
}
printf("\n");
}
getch();
return 0;
}
Program Output
Enter size square matrix 2 Enter Matrix of size 2X2 1 1 1 1 Lower triangular Matrix 1 0 1 1
Enter size square matrix 3 Enter Matrix of size 3X3 1 2 3 4 5 6 7 8 9 Lower triangular Matrix 1 0 0 4 5 0 7 8 9
Properties of lower triangular matrix
- The sum of two lower triangular matrices is lower triangular.
- The product of two lower triangular matrices is lower triangular.
- The inverse of a lower triangular matrix is a lower triangular.
- The eigenvalues of a lower triangular matrix are the diagonal elements.
