C Program to Print Fibonacci Series using Recursion

• Write a c program to print fibonacci series using recursion

Fibonacci series are the numbers in the following integer sequence
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ….
the first two numbers in the Fibonacci sequence are 0 and 1, and each subsequent term is the sum of the previous two terms. In mathematical terms, the Nth term of Fibonacci numbers is defined by the recurrence relation:

• fibonacci(N) = Nth term in fibonacci series
• fibonacci(N) = fibonacci(N – 1) + fibonacci(N – 2);
• whereas, fibonacci(0) = 0 and fibonacci(1) = 1

Below program uses recursion to calculate Nth fibonacci number. To calculate Nth fibonacci number it first calculate (N-1)th and (N-2)th fibonacci number and then add both to get Nth fibonacci number.
For Example : fibonacci(4) = fibonacci(3) + fibonacci(2);

C program to print fibonacci series till Nth term using recursion

In below program, we first takes the number of terms of fibonacci series as input from user using scanf function. We are using a user defined recursive function named ‘fibonacci’ which takes an integer(N) as input and returns the N^th fibonacci number using recursion as discussed above. The recursion will terminate when number of terms are < 2 because we know the first two terms of fibonacci series are 0 and 1.In line number 17, we are calling this function inside a for loop to get the N^th term of series.

/*
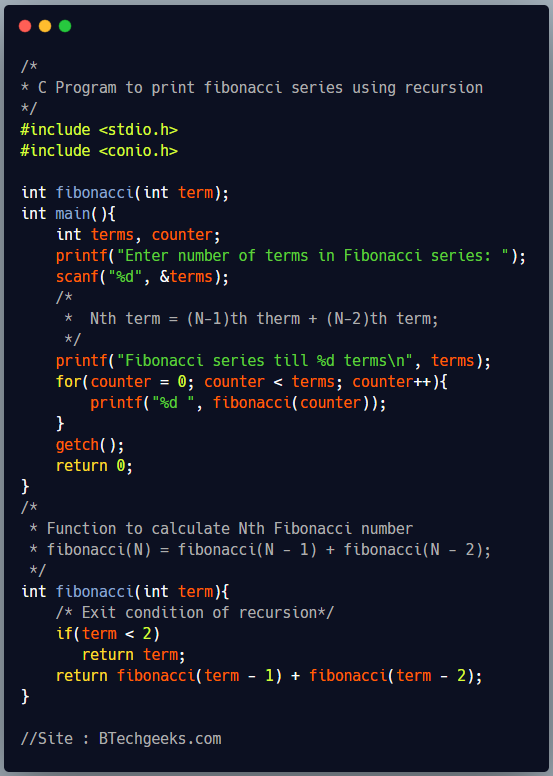
* C Program to print fibonacci series using recursion
*/
#include <stdio.h>
#include <conio.h>
 
int fibonacci(int term);
int main(){
    int terms, counter;
    printf("Enter number of terms in Fibonacci series: ");
    scanf("%d", &terms);
    /*
     *  Nth term = (N-1)th therm + (N-2)th term;
     */
    printf("Fibonacci series till %d terms\n", terms); 
    for(counter = 0; counter < terms; counter++){
        printf("%d ", fibonacci(counter));
    }
    getch();
    return 0;
}
/*
 * Function to calculate Nth Fibonacci number
 * fibonacci(N) = fibonacci(N - 1) + fibonacci(N - 2);
 */
int fibonacci(int term){
    /* Exit condition of recursion*/
    if(term < 2)
       return term;
    return fibonacci(term - 1) + fibonacci(term - 2);
}

Program Output

Enter number of terms in Fibonacci series: 9
Fibonacci series till 9 terms
0 1 1 2 3 5 8 13 21

Fibonacci series till Nth term using memorization

Recursive program to print fibonacci series is not so efficient because it does lots of repeated work by recalculating lower terms again and again.

For Example:
fibonacci(6) = fibonacci(5) + fibonacci(4);
To calculate fibonacci(5) it will calculate fibonacci(4) and fibonacci(3). Now, while calculating fibonacci(4) it will again calculate fibonacci(3) which we already calculated while calculating fibonacci(5). We can solve this recalculation problem by memorizing the already calculated terms in an array.

In the below program, we are using an integer array named ‘fibonacciArray’ to store the already calculated terms of fibonacci series(N^th term of fibonacci series is stored at fibonacciArray[N-1]). To calculate the N^th term we add the last two fibinacci elements(N-1 and N-2^th element) stored in array. Finally we store the N^th term also in array so that we can use it to calculate next fibonacci elements.

/*
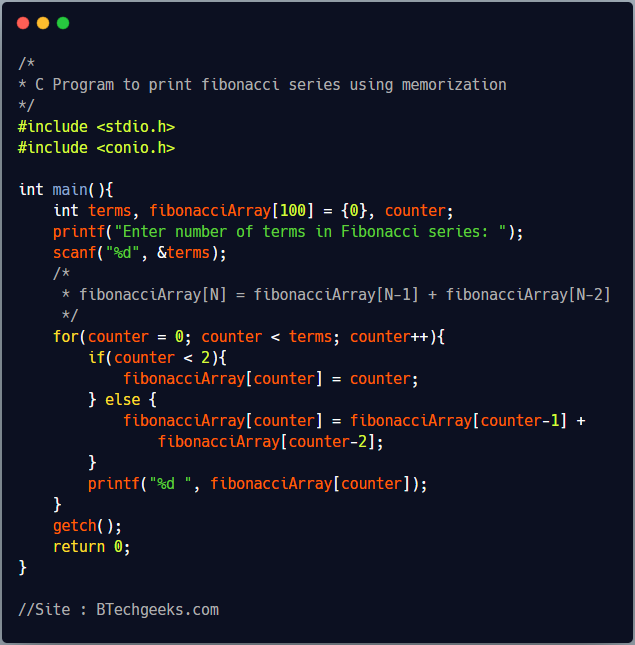
* C Program to print fibonacci series using memorization
*/
#include <stdio.h>
#include <conio.h>
  
int main(){
    int terms, fibonacciArray[100] = {0}, counter;
    printf("Enter number of terms in Fibonacci series: ");
    scanf("%d", &terms);
    /*
     * fibonacciArray[N] = fibonacciArray[N-1] + fibonacciArray[N-2]
     */
    for(counter = 0; counter < terms; counter++){
        if(counter < 2){
            fibonacciArray[counter] = counter;
        } else {
            fibonacciArray[counter] = fibonacciArray[counter-1] +
                fibonacciArray[counter-2];
        }
        printf("%d ", fibonacciArray[counter]);
    }
    getch();
    return 0;
}

Program Output

Enter number of terms in Fibonacci series: 7
Fibonacci series till 7 terms
0 1 1 2 3 5 8