C Program to find Value of nPr and nCr

Write a C program to find the value of nPr and nCr

nPr is the number of ways of obtaining an ordered subset of r elements from a set of n elements. Parameter n stands for the number of items in the complete set whereas r stands for the number of items you want to select. In other words, nPr means number of ways you can select r items from set of n items where order makes difference.

nPr = n!/(n-r)!

Where n!, denotes the factorial of a number, it is the product of all positive integers less than or equal to n. Factorial does not exist for negative numbers and factorial of 0 is 1. Its most basic occurrence is the fact that there are n! ways to arrange n distinct objects into a sequence. Hence, to calculate nPr, we have to calculate factorial of n and (n-r) and divides them as per above expression.

Before proceeding, I will recommend to check Factorial program first : Factorial Program in C

C program to find nPr using function.

In this program we first take n and r as input form user. As per definition of nPr, n >= r. Which means, If a set contains n items then you cannot select more than n items from that set. Here we are using a user defined function getFactorial(N), which takes a number as input and return its factorial value. Function getNPR calls getFactorial function to calculate numerator and denominator or nPr expression.

/*
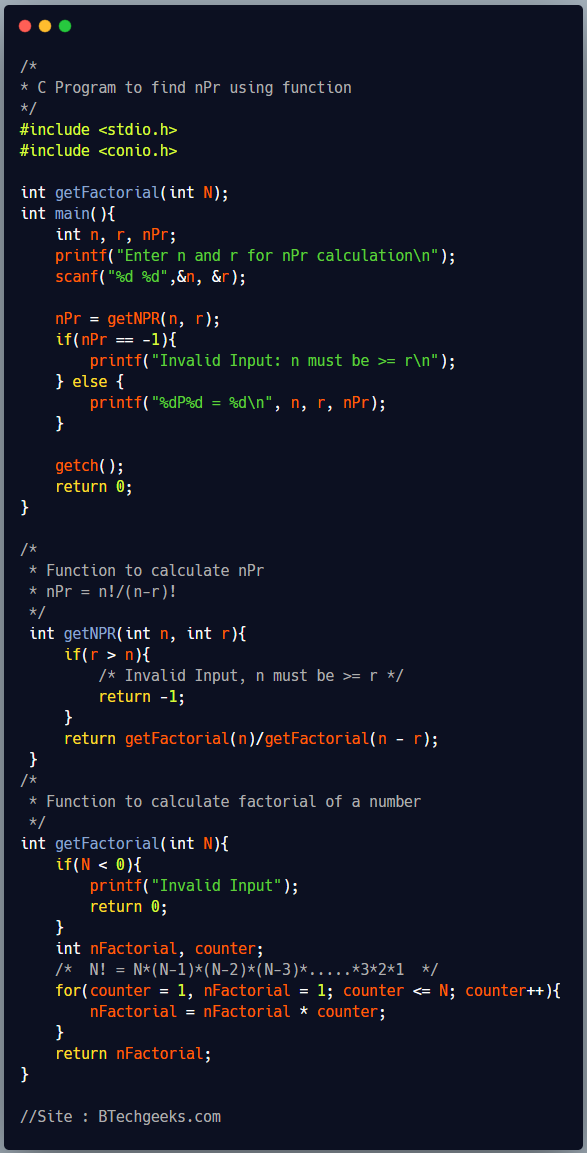
* C Program to find nPr using function
*/
#include <stdio.h>
#include <conio.h>
 
int getFactorial(int N);
int main(){
    int n, r, nPr;
    printf("Enter n and r for nPr calculation\n");
    scanf("%d %d",&n, &r);
 
    nPr = getNPR(n, r);
    if(nPr == -1){
        printf("Invalid Input: n must be >= r\n");
    } else {
        printf("%dP%d = %d\n", n, r, nPr);
    }
     
    getch();
    return 0;
}
 
/*
 * Function to calculate nPr 
 * nPr = n!/(n-r)!
 */
 int getNPR(int n, int r){
     if(r > n){
         /* Invalid Input, n must be >= r */
         return -1;
     }
     return getFactorial(n)/getFactorial(n - r);
 }
/*
 * Function to calculate factorial of a number 
 */
int getFactorial(int N){
    if(N < 0){
        printf("Invalid Input");
        return 0;
    }
    int nFactorial, counter;
    /*  N! = N*(N-1)*(N-2)*(N-3)*.....*3*2*1  */
    for(counter = 1, nFactorial = 1; counter <= N; counter++){
        nFactorial = nFactorial * counter;
    }    
    return nFactorial;
}

Program Output

Enter n and r for nPr calculation
6 2
6P2 = 30

C program to find nCr using a function

nCr means number of ways you can select r items from set of n items where order makes no difference. It defines, IN how many ways we can select a small group from a larger group.
For Example:
In how many ways you can select a group of five employees from an office of 20 employees.

Points to Remember

If the order doesn’t matter, it is a Combination.
If the order does matter it is a Permutation.

nCr = n!/(r!*(n-r)!)
nCr = nPr/r!

If you have nPr, then divide it with r! to get nCr.

/*
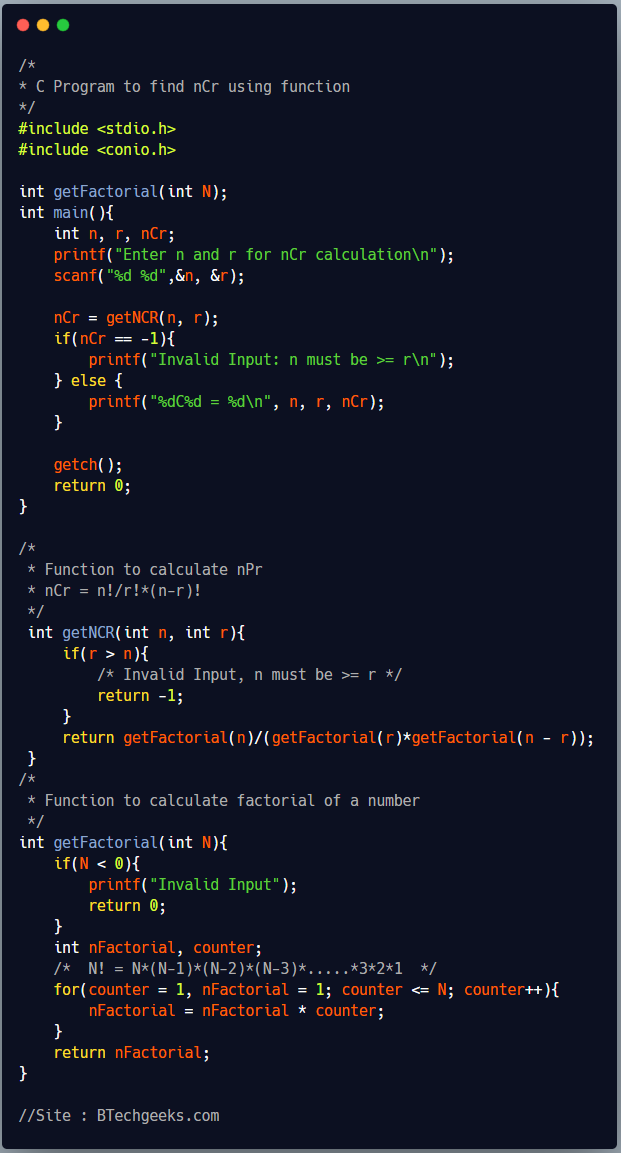
* C Program to find nCr using function
*/
#include <stdio.h>
#include <conio.h>
 
int getFactorial(int N);
int main(){
    int n, r, nCr;
    printf("Enter n and r for nCr calculation\n");
    scanf("%d %d",&n, &r);
 
    nCr = getNCR(n, r);
    if(nCr == -1){
        printf("Invalid Input: n must be >= r\n");
    } else {
        printf("%dC%d = %d\n", n, r, nCr);
    }
     
    getch();
    return 0;
}
 
/*
 * Function to calculate nPr 
 * nCr = n!/r!*(n-r)!
 */
 int getNCR(int n, int r){
     if(r > n){
         /* Invalid Input, n must be >= r */
         return -1;
     }
     return getFactorial(n)/(getFactorial(r)*getFactorial(n - r));
 }
/*
 * Function to calculate factorial of a number 
 */
int getFactorial(int N){
    if(N < 0){
        printf("Invalid Input");
        return 0;
    }
    int nFactorial, counter;
    /*  N! = N*(N-1)*(N-2)*(N-3)*.....*3*2*1  */
    for(counter = 1, nFactorial = 1; counter <= N; counter++){
        nFactorial = nFactorial * counter;
    }    
    return nFactorial;
}

Program Output

Enter n and r for nCr calculation
6 2
6C2 = 15

C program to find nPr using function.

C program to find nCr using a function

Related