C Program to Find Power of a Number using Recursion

• Write a C program to find power of a number(a^b) using recursion.

The power of a number(base^exponent)is the base multiplied to itself exponent times.
For Example
a^b = a x a x a …..x a(b times)
2⁴ = 2x2x2x2 = 16

Here we will solve this problem using recursion. We will first take base and exponent as input from user and pass it to a recursive function, which will return the value of base raised to the power of exponent(base^exponent).

Algorithm to find power of a number using recursion

• Base condition of recursion : A⁰ = 1; (anything to the power of 0 is 1).
• To calculate Aⁿ, we can first calculate A^n-1 and then multiply it with A(A^n = A X A^n-1).
• Let getPower(int A, int n) is a function which returns Aⁿ. Then we can write recursive expression as getPower(A, n) = A X getPower(A, n-1);

Time Complexity: O(n)

C program to find power of a number using recursion

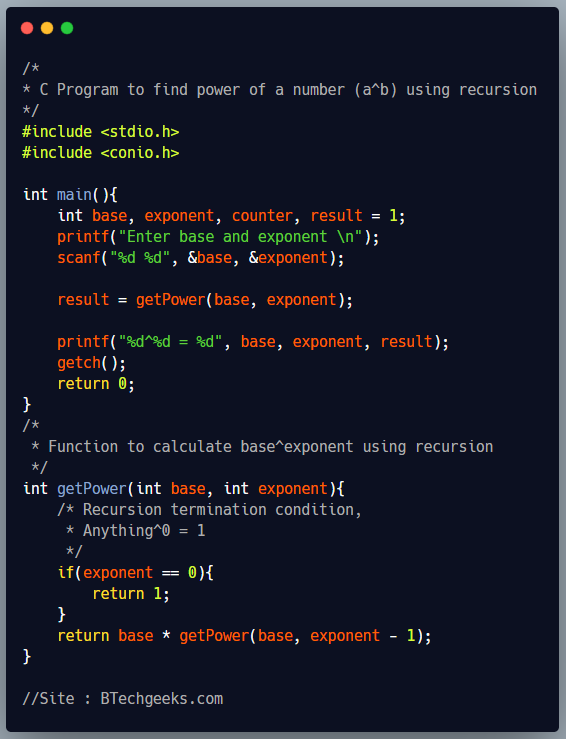
Below program first takes base and exponent as input from user using scanf function and stores it in integer variables. It uses a user defined function getPower, that takes base and exponent as input parameters and returns the value of base^exponent. To calculate base^exponent, function getPower calls itself recursively as getPower(base, exponent-1) to calculate base^exponent-1
For Example:
2³ = getPower(2,3) = 2 x getPower(2,2) = 2 x 2 x getPower(2,1) = 2 x 2 x 2 x getPower(2,0) = 2 x 2 x 2 x 1 = 8

/*
* C Program to find power of a number (a^b) using recursion
*/
#include <stdio.h>
#include <conio.h>
 
int main(){
    int base, exponent, counter, result = 1;
    printf("Enter base and exponent \n");
    scanf("%d %d", &base, &exponent);
     
    result = getPower(base, exponent);
     
    printf("%d^%d = %d", base, exponent, result);
    getch();
    return 0;
}
/*
 * Function to calculate base^exponent using recursion
 */
int getPower(int base, int exponent){
    /* Recursion termination condition,
     * Anything^0 = 1
     */
    if(exponent == 0){
        return 1;
    }
    return base * getPower(base, exponent - 1);
}

Program Output

Enter base and exponent 
4 0
4^0 = 1

Enter base and exponent 
3 4
3^4 = 81

C program to find power of a number using divide and conquer

To find the power of a number, we can use Divide and Conquer approach. A divide and conquer algorithm solves a problem in three steps.

• It divides a problem into two or more sub problems. Such that each sub-problem is same as the original problem but for smaller data set.
• It solve each sub-problem recursively and stores the solution of each sub-problem If required.
• It combines the solutions of sub-problem to get the overall solution of original problem.

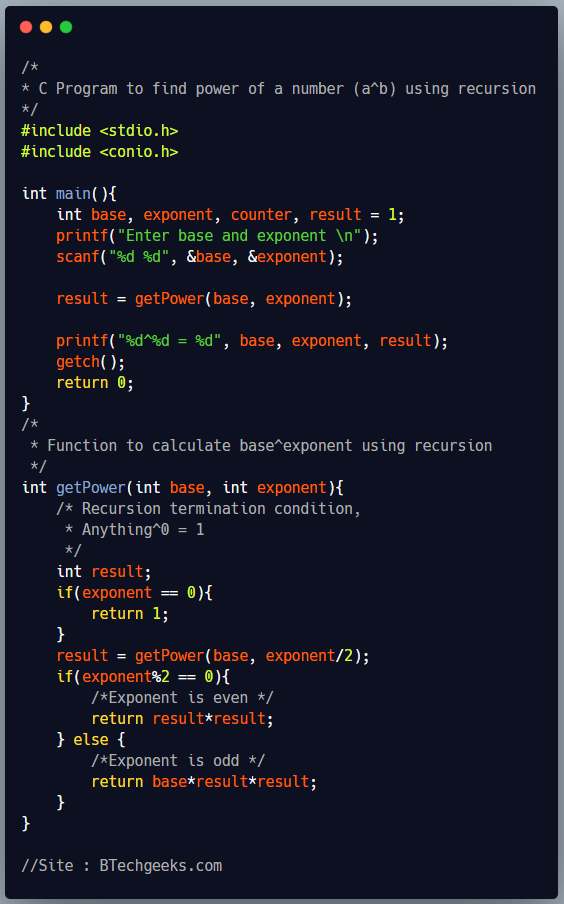
Below program contains a user defined function getPower, that takes base and exponent as input parameters and returns the value of base^exponent. Function getPower implements the divide and conquer algorithm mentioned above to calculate the power of a number.

getPower(A, n) = if n is even: getPower(A, n-1) X getPower(A, n-1); 
                 if n is odd: A X getPower(A, n-1) X getPower(A, n-1);

/*
* C Program to find power of a number (a^b) using recursion
*/
#include <stdio.h>
#include <conio.h>
 
int main(){
    int base, exponent, counter, result = 1;
    printf("Enter base and exponent \n");
    scanf("%d %d", &base, &exponent);
     
    result = getPower(base, exponent);
     
    printf("%d^%d = %d", base, exponent, result);
    getch();
    return 0;
}
/*
 * Function to calculate base^exponent using recursion
 */
int getPower(int base, int exponent){
    /* Recursion termination condition,
     * Anything^0 = 1
     */
    int result;
    if(exponent == 0){
        return 1;
    }
    result = getPower(base, exponent/2);
    if(exponent%2 == 0){
        /*Exponent is even */
        return result*result;
    } else {
        /*Exponent is odd */
        return base*result*result;
    }
}

Program Output

Enter base and exponent 
5 4
5^4 = 625