C Program to Find Hcf and Lcm of Two Numbers

Write a C program to find LCM and HCF of two numbers

The least common multiple(LCM) of two integers a and b, usually denoted by LCM (a, b), is the smallest positive integer that is divisible by both a and b.

Algorithm to find LCM of two number

Find the prime factorization of each of the two numbers.
48 = 2 × 2 × 2 × 2 × 3;
180 = 2 × 2 × 3 × 3 × 5;
Create set of prime factor for both numbers.
Set-48 = {2, 2, 2, 2, 3}
Set-180 = {2, 2, 3, 3, 5}
Find common elements in both set.
Set-Common = {2, 2, 3}
Now Combine elements of Set-48 and Set-180 in one set.
Set-Combined = Set-48 and Set-180
Set-Combined = {2, 2, 2, 2, 3} + {2, 2, 3, 3, 5}
Set-Combined = {2, 2, 2, 2, 2, 2, 3, 3, 3, 5}
Now, Set-LCM = Set-Combined – Set-Common
Set-LCM = {2, 2, 2, 2, 2, 2, 3, 3, 3, 5} – {2, 2, 3}
Set-LCM = {2, 2, 2, 2, 3, 3, 5}
LCM (48, 180) = Product of all elements of Set-LCM
LCM (48, 180) = 2 × 2 × 2 × 2 × 3 × 3 × 5
LCM (48, 180) = 720

The highest common factor(HCF) of two or more integers, is the largest positive integer that divides the numbers without a remainder. HCF is also known as greatest common divisor(GCD) or greatest common factor(GCF).

Algorithm to find HCF or GCD of two number

Find the prime factorization of each of the two numbers.
48 = 2 × 2 × 2 × 2 × 3;
180 = 2 × 2 × 3 × 3 × 5;
Create set of prime factor for both numbers.
Set-48 = {2, 2, 2, 2, 3}
Set-180 = {2, 2, 3, 3, 5}
Find common elements in both set.
Set-Common = {2, 2, 3}
GCD (48, 180) = Product of all elements of Set-Common
GCD (48, 180) = 2 × 2 × 3
GCD (48, 180) = 12

If we know LCM or HCF of two numbers, then we can find the other one using below equation.

LCM(A, B) X HCF(A, B) = A*B

C program to find LCM and HCF of two numbers using loop

/*
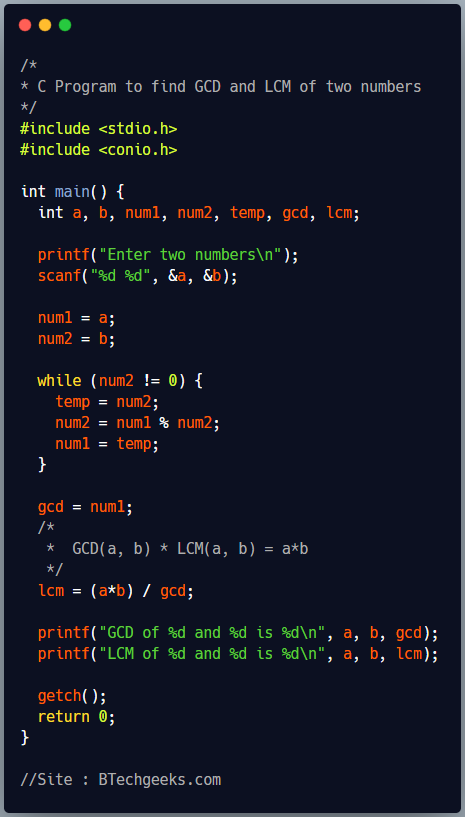
* C Program to find GCD and LCM of two numbers
*/
#include <stdio.h>
#include <conio.h>
 
int main() {
  int a, b, num1, num2, temp, gcd, lcm;
  
  printf("Enter two numbers\n");
  scanf("%d %d", &a, &b);
 
  num1 = a;
  num2 = b;
  
  while (num2 != 0) {
    temp = num2;
    num2 = num1 % num2;
    num1 = temp;
  }
  
  gcd = num1;
  /* 
   *  GCD(a, b) * LCM(a, b) = a*b  
   */
  lcm = (a*b) / gcd;
  
  printf("GCD of %d and %d is %d\n", a, b, gcd);
  printf("LCM of %d and %d is %d\n", a, b, lcm);
   
  getch();
  return 0;
}

Program Output

Enter two numbers
48 180
GCD of 48 and 180 is 12
LCM of 48 and 180 is 720

C program to find LCM and HCF of two numbers using recursion

/*
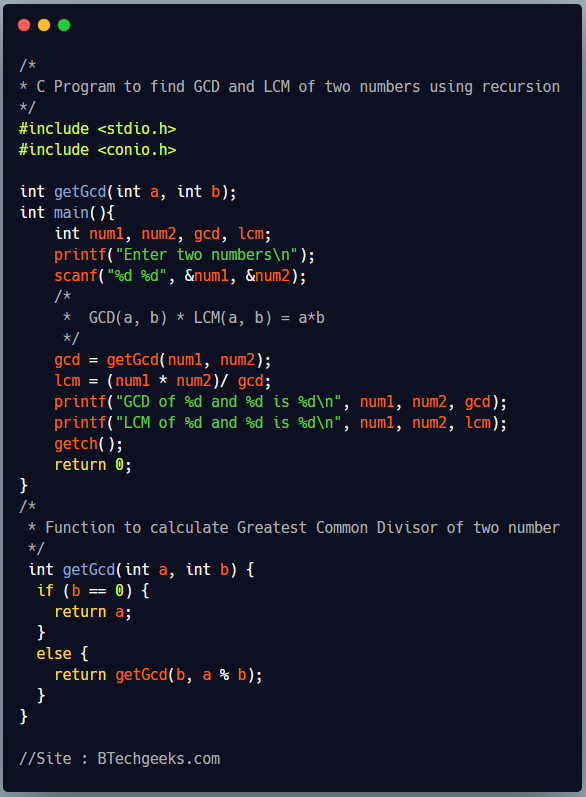
* C Program to find GCD and LCM of two numbers using recursion
*/
#include <stdio.h>
#include <conio.h>
  
int getGcd(int a, int b);
int main(){
    int num1, num2, gcd, lcm;
    printf("Enter two numbers\n");
    scanf("%d %d", &num1, &num2);
    /*
     *  GCD(a, b) * LCM(a, b) = a*b  
     */
    gcd = getGcd(num1, num2);
    lcm = (num1 * num2)/ gcd;
    printf("GCD of %d and %d is %d\n", num1, num2, gcd);
    printf("LCM of %d and %d is %d\n", num1, num2, lcm);
    getch();
    return 0;
}
/*
 * Function to calculate Greatest Common Divisor of two number
 */
 int getGcd(int a, int b) {
  if (b == 0) {
    return a;
  }
  else {
    return getGcd(b, a % b);
  }
}

Program Output

Enter two numbers
4 38
GCD of 48 and 180 is 2
LCM of 48 and 180 is 76

C program to find LCM and HCF of two numbers using loop

C program to find LCM and HCF of two numbers using recursion

Related