- Write a C program to find roots of a quadratic equation.
A quadratic equation is a second order equation having a single variable. Any quadratic equation can be represented as ax2 + bx + c = 0, where a, b and c are constants( a can’t be 0) and x is unknown variable.
For Example
2x2 + 5x + 3 = 0 is a quadratic equation where a, b and c are 2, 5 and 3 respectively.
To calculate the roots of quadratic equation we can use below formula. There are two solutions of a quadratic equation.
x = (-2a + sqrt(D))/2
x = (-2a – sqrt(D))/2
where, D is Discriminant, which differentiate the nature of the roots of quadratic equation.
| Discriminant(D) value | Description |
|---|---|
| D < 0 | We will get two complex roots. |
| D = 0 | We will get two equal roots. |
| D > 0 | We will get two real numbers. |
C program to find all roots of a quadratic equation
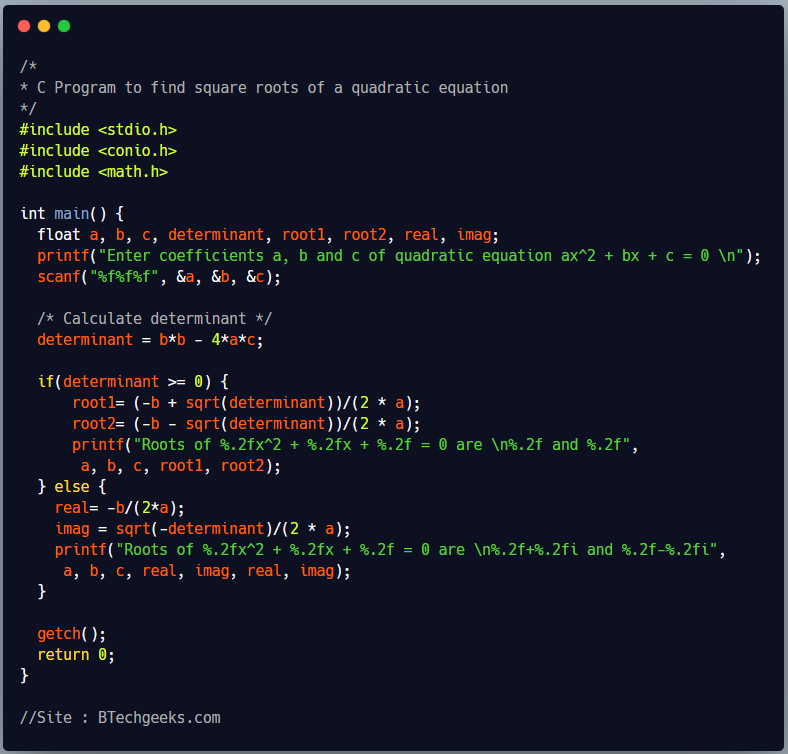
/*
* C Program to find square roots of a quadratic equation
*/
#include <stdio.h>
#include <conio.h>
#include <math.h>
int main() {
float a, b, c, determinant, root1, root2, real, imag;
printf("Enter coefficients a, b and c of quadratic equation ax^2 + bx + c = 0 \n");
scanf("%f%f%f", &a, &b, &c);
/* Calculate determinant */
determinant = b*b - 4*a*c;
if(determinant >= 0) {
root1= (-b + sqrt(determinant))/(2 * a);
root2= (-b - sqrt(determinant))/(2 * a);
printf("Roots of %.2fx^2 + %.2fx + %.2f = 0 are \n%.2f and %.2f",
a, b, c, root1, root2);
} else {
real= -b/(2*a);
imag = sqrt(-determinant)/(2 * a);
printf("Roots of %.2fx^2 + %.2fx + %.2f = 0 are \n%.2f+%.2fi and %.2f-%.2fi",
a, b, c, real, imag, real, imag);
}
getch();
return 0;
}
Program Output
Enter coefficients a, b and c of quadratic equation ax^2 + bx + c = 0 1 1 1 Roots of 1.00x^2 + 1.00x + 1.00 = 0 are -0.50+0.87i and -0.50-0.87i Enter coefficients a, b and c of quadratic equation ax^2 + bx + c = 0 3 7 2 Roots of 3.00x^2 + 7.00x + 2.00 = 0 are -0.33 and -2.00
