- Write a C program to find the area and perimeter of a parallelogram.
A parallelogram is quadrilaterals(having four sides) with opposite sides parallel and equal in length. Opposite angles of a parallelogram are also equal.
The area of parallelogram is the amount of two-dimensional space inside it’s boundary. The area of a parallelogram can be calculated by placing the parallelogram over a grid and counting the number of square units it takes to completely fill a parallelogram.
Properties of Parallelogram
- Diagonals of a parallelogram divides each other in two equal half.
- Opposite sides of a parallelogram are parallel and equal in length.
- Opposite angles of a parallelogram are equal.
- The sum of any two adjacent angles of a parallelogram are 180 degrees.
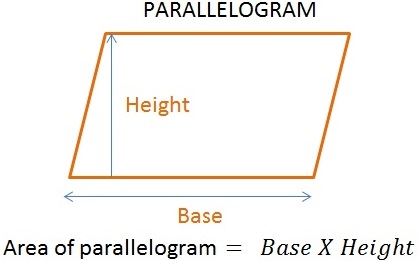
To calculate the area of parallelogram we need length of Base and Height.
Base : We can choose any side of a parallelogram as base to calculate area of parallelogram.
Height : Height of a parallelogram is the perpendicular distance between the base and it’s opposite side.
Area of Parallelogram
The area of a parallelogram can be calculated by multiplying Base and Height.
- Area of Parallelogram = B X H
Where,
B is the length of base of parallelogram.
H is the length of height of parallelogram.
(Base and Height are perpendicular on each other)
Perimeter of Parallelogram
The perimeter of a parallelogram can be calculated by adding the length of all four sides of parallelogram. As we know the length of opposite sides of parallelogram are equal, we can add any two adjacent sides of parallelogram and then multiply it with 2 to get perimeter of parallelogram.
- Perimeter of Parallelogram = 2X(S1 + S2)
Where,
S1 and S2 are length of adjacent sides of parallelogram.
C program to find the area of the parallelogram
To find the area of a parallelogram we need to the length of it’s Base and Height. Below program, first takes length of base and height as input from user using scanf function and stores it in floating point variable. Now, we multiple base and height of parallelogram to get it’s area as per formula given above. Finally it prints the area on screen using printf function.
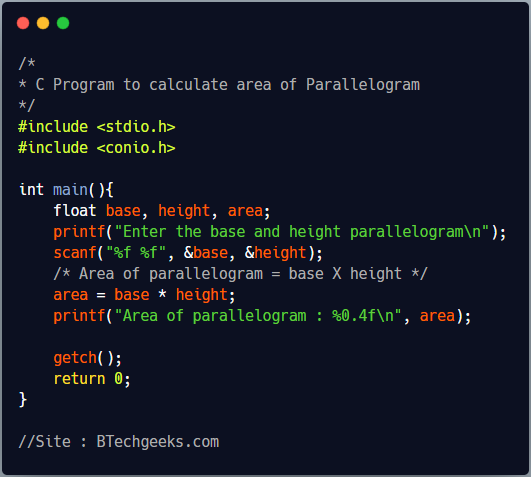
/*
* C Program to calculate area of Parallelogram
*/
#include <stdio.h>
#include <conio.h>
int main(){
float base, height, area;
printf("Enter the base and height parallelogram\n");
scanf("%f %f", &base, &height);
/* Area of parallelogram = base X height */
area = base * height;
printf("Area of parallelogram : %0.4f\n", area);
getch();
return 0;
}
Program Output
Enter the base and height parallelogram 5 3.5 Area of parallelogram : 17.5000
C program to find perimeter of the parallelogram
To find the perimeter of a parallelogram we need to the length of adjacent sides of a parallelogram. Below program, first takes length of two sides as input from user using scanf function and stores it in floating point variable. Now, we add length of both sides of parallelogram and multiply it with 2 to get it’s perimeter as per formula given above. Finally it prints the perimeter on screen using printf function.
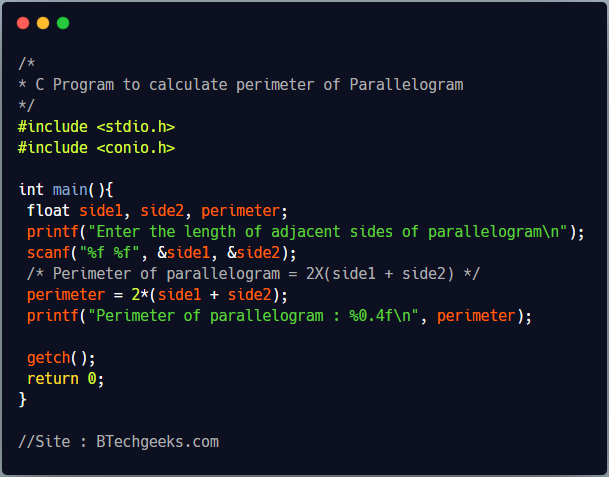
/*
* C Program to calculate perimeter of Parallelogram
*/
#include <stdio.h>
#include <conio.h>
int main(){
float side1, side2, perimeter;
printf("Enter the length of adjacent sides of parallelogram\n");
scanf("%f %f", &side1, &side2);
/* Perimeter of parallelogram = 2X(side1 + side2) */
perimeter = 2*(side1 + side2);
printf("Perimeter of parallelogram : %0.4f\n", perimeter);
getch();
return 0;
}
Program Output
Enter the length of adjacent sides of parallelogram 4.0 3.0 Perimeter of parallelogram : 14.0000
Interesting Facts about Parallelogram
- A line passing through the midpoint of a parallelogram always divides the parallelogram into two sections of equal areas.
- A diagonal of a parallelogram divides a parallelogram into two congruent triangles(all sides and angles equal).
- If you connect the mid points of any quadrilateral with line segments then the resulting quadrilateral is always a parallelogram.
- A rectangle is a special case of parallelogram with all angles measure 90 degree.
- A square is also a special case of parallelogram with all sides and angles equal.
- A rhombus is also a parallelogram with all sides equal.
